Зависимость спектральной плотности сигнала от масштаба времени

Сигнал S(t) может быть подвергнут сжатию или растяжению по времени. Если вместь переменной t ввести переменную kt, где – некоторое вещеcтвенное число, то при 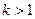происходит сжатие исходного сигнала, а при 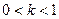происходит растяжение исходного сигнала S(t).

Пусть для сигнала S(t) справедливо преобразование Фурье 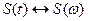, т.е. можно сказать, что сигнал S(t) имеет спектральную плотность S(w), тогда:

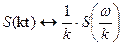
Доказательство

Сигнал S (t) имеет спектральную плотность S (w), то есть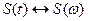. Пусть сигнал S(kt) имеет некоторую спектральную плотность 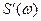, значит справедливо преобразование Фурье 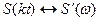. Определим..

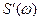Введем переменную 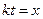и получим,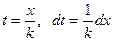

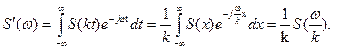
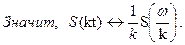
При сжатии сигнала в 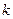раз во времени во столько же раз расширяется его спектр.