Спектральная плотность производной и неопределенного интеграла

Пусть для сигнала S (t) справедливо преобразование Фурье 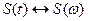, т.е. можно сказать, что сигнал S (t) имеет спектральную плотность S (w). Спектральная плотность сигнала F (t), представляющего собой производную сигнала S (t), то есть 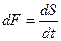, определяется следующим образом:

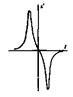
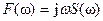
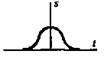исходный сигнал S (t)

дифференцированный сигнал

(при дифференцировании определяется скорость измен сигнала)

Дифференцирование сигнала во времени соответствует умножению спектральной плотности на множитель 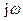. Множитель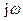называется оператором дифференцирования в частотной области.

Сигнал S (t) является первообразной для сигнала F (t):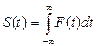

Тогда спектр первообразной .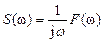

Множитель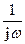называется оператором интегрирования в частотной области.