Пусть для сигналов 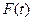 і
і 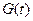 известны соответствия
известны соответствия 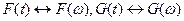 , а сигнал S (t) является произведением
, а сигнал S (t) является произведением 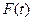 и
и 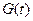 .
.
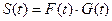
Тогда спектральная плотность:
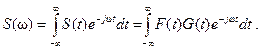
Выразим черезинтеграл Фурье
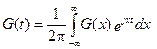
Тогда,
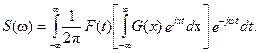
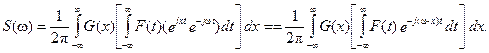
Выражение в квадратных скобках является спектром сигнала F(t), сдвинутым на величину x.
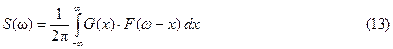
Интеграл в правой части выражения (13) называется сверткой функций F( 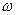 ) и G(
) и G( 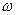 ).
).
Операция свертки обозначается таким образом:
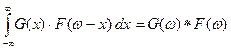
Таким образом, можно сказать, что спектральная плотность произведения двух сигналов с точностью до постоянного коэффициента равна свертке спектральных плотностей этих сигналов:
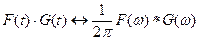
Существует и обратная теорема: Если спектральная плотность некоторого сигнала может быть представлена в виде произведения 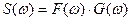 причем
причем 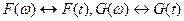 , то сигнал
, то сигнал 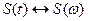 является сверткой сигналов F(t) и G(t).
является сверткой сигналов F(t) и G(t).
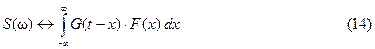
6) Средняя мощность для периодического сигнала определяется теоремой Парсеваля как сумма мощностей всех компонент, из которых складывается обобщенный ряд Фурье.
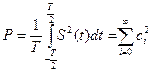 , где
, где 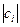 являются
являются
комплексными коэффициентами ряда Фурье для периодического сигнала.
7) Энергия для непериодического сигнала:
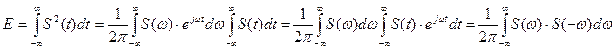
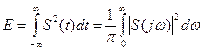
Величина 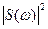 называется спектральной плотностью энергии сигнала. Эта формула используется для определения практической ширины спектра сигнала.
называется спектральной плотностью энергии сигнала. Эта формула используется для определения практической ширины спектра сигнала.
Практическая ширина спектра сигнала должна быть такой, чтобы с заданной точностью выполнялось равенство:
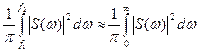
 2014-02-03
2014-02-03 2179
2179
