Спектральная плотность суммы сигналов.
Исходя из того, что преобразование Фурье является линейным, при сложении сигналов S 1(t) і S 2(t), которые имеют спектры S 1(w) і S 2(w), суммарный сигнал S (t)= S 1(t)+ S 2(t) будет иметь спектр S (w) = S 1(w) + S 2(w).
Пусть для сигнала S (t) справедливо преобразование Фурье 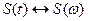 , т.е. можно сказать, что сигнал S (t) имеет спектральную плотность S (w), то есть:
, т.е. можно сказать, что сигнал S (t) имеет спектральную плотность S (w), то есть:
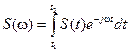
При задержке этого сигнала на время t 0 получаем новую функцию 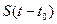 . Пусть этот сигнал имеет некоторую спектральную плотность
. Пусть этот сигнал имеет некоторую спектральную плотность 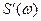 , значит справедливо преобразование Фурье
, значит справедливо преобразование Фурье 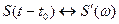 . Определим
. Определим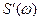 .
.
Введем 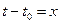 и получим
и получим
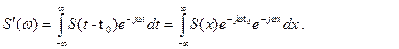
Но 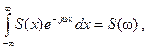 значит
значит 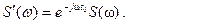
А это означает, что сдвиг по времени функции S(t) на 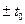 приводит к изменению фазовой характеристики спектра S(w) на величину
приводит к изменению фазовой характеристики спектра S(w) на величину 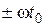 . Модуль спектральной плотности от положения сигнала на временной оси не зависит.
. Модуль спектральной плотности от положения сигнала на временной оси не зависит.
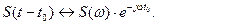
 2014-02-03
2014-02-03 1329
1329








