СОДЕРЖАНИЕ
Рис.31.1
Таблица 3.2
Классификация
Системы автоматического управления (САУ) достаточно разнообразны, однако они поддаются четкой классификации по следующим признакам:
1. По виду уравнений динамики процессов управления: линейные и нелинейные.
2. По закону изменения входного сигнала x:
- системы автоматической стабилизации (x=const); примеры: САР частоты вращения дизеля; САУ курсом судна в режиме "Автомат";
- системы программного управления (закон изменения x заранее известен); пример: САР стерилизации консервов в автоклаве;
- следящие системы (x изменяется по произвольному закону); пример: САУ курсом судна в режиме "Следящий".
3. По виду используемого регулятора:
- линейные, нелинейные, импульсные и цифровые САУ.
4. По общему алгоритму функционирования:
- обычные САУ; оптимальные и адаптивные САУ.
1.2. Принципы автоматического управления
Основополагающими понятиями САУ являются:
· состав и характеристики входных сигналов, которые подразделяются на сигналы управления и сигналы возмущения;
· совокупность показателей качества регулирования выходного сигнала;
· структурная схема САУ и динамические характеристики звеньев САУ.
Все многообразие САУ может быть сведено к 3-м элементарным схемам управления, называемых также принципами управления: прямое управление, управление по возмущению, управление по отклонению.
1.2.1. Принцип прямого управления (рис.1.2)
 |
Особенности: За выходным сигналом y следит человек-оператор, который вручную изменяет x так, чтобы достичь заданных значений сигнала y. Сигналы возмущения g1-g6, изменяющие произвольным образом выходной сигнал y, человеком не контролируются.
Достоинства: Предельная простота регулятора.
Недостатки: 1. Обязательное присутствие оператора.
2. Малая точность, невысокое быстродействие.
3. Отсутствие компенсации внешних возмущений.
Пример: Электропривод якорно-швартового устройства. Оператор с помощью соответствующих органов управления задаёт одну из фиксированных скоростей вращения двигателя. Сигналами возмущения g1–g6 являются: натяжение якорной цепи, напряжение питания электродвигателя, температура обмоток двигателя и др.
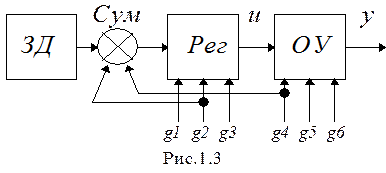 |
1.2.2. Принцип управления по возмущению (рис.1.3)
Особенности: Некоторые из сигналов возмущения, которые можно измерить и преобразовать в электрический сигнал (если регулятор электрический), заводятся на вход регулятора через сумматор Сум. Это приводит к такому изменению выходного сигнала регулятора u, при котором компенсируется действие на систему измеренных сигналов возмущения.
Достоинства: 1. Наивысшее быстродействие в сравнении с другими схемами.
2. Выше точность регулирования в сравнении с прямым управлением.
Недостатки: 1. Сложность выделения всех возмущений, действующих на элементы САУ. Сложность их классификации на основные и второстепенные.
2. Сложность измерения и преобразования сигналов возмущения в электрический сигнал. Например, чрезвычайно сложной является задача измерения механического момента в валах вращающихся механизмов.
Пример: САР напряжения генератора (система токового компаундирования). Регулируемый сигнал – напряжение на выводах генератора. Возмущающий сигнал – ток нагрузки генератора, который измеряется просто трансформатором тока.
1.2.3. Принцип управления по отклонению (рис.1.4)
Особенности: Вводится цепь обратной связи ОС и элемент сравнения ЭС, на котором вычитаются заданное значение x и фактическое значение y регулируемого сигнала. В ЭС формируется ошибка регулирования e. Регулятор Рег вырабатывает такой сигнал u, который уменьшает ошибку регулирования e.
Достоинства: 1. Нет необходимости в выяснении того, какие сигналы возмущения действуют на САУ, и, следовательно, не нужно их измерять.
2. Самая высокая точность регулирования в сравнении с другими схемами САУ.
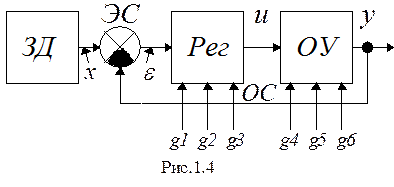 |
Недостатки:
Меньше в сравнении с управлением по возмущению быстродействие, т.к. регулирующий сигнал u начинает изменяться не в момент появления возмущений, а только после изменения y.
Примеры:
1. Авторулевой, удерживающий судно на заданном курсе с требуемой точностью в условиях волнения моря и других возмущающих сигналах.
2. Электропривод траловой лебедки, обеспечивающий требуемые усилия и скорость выборки трала в условиях переменной нагрузки на ваерах, волнения моря, действия течений.
3. Холодильная автоматика, обеспечивающая поддержание заданной температуры в камерах в условиях изменяющегося притока тепла.
Достоинства схемы управления по отклонению настолько велики, что САУ в подавляющем числе случаев выполняются работающими именно по этой схеме.
ТЕОРИЯ ЛИНЕЙНЫХ САУ
2.Линеаризация уравнений элементов САУ.
Преобразование Лапласа. Передаточная функция.
Типовые воздействия и реакция на них.
2.1. Линеаризация дифференциальных уравнений
Все возможные элементы САУ характеризуются набором входных и выходных сигналов. Общее название элементов - звенья. Для того чтобы решать задачи методами ТАУ звенья должны быть описаны, в общем случае, дифференциальными и, в редких случаях - алгебраическими уравнениями.
Так как все методы и результаты автоматики базируются на свойствах решений дифференциальных уравнений, то первостепенное значение имеет умение просто и быстро решать дифференциальные уравнения.
Наиболее простыми и систематически проработанными являются методы решения линейных дифференциальных уравнений. Результаты, полученные в линейных САУ, широко используются также в расчётах нелинейных и импульсных систем.
 |
Если не накладывать ограничений на пределы изменения входных сигналов реальных, физических объектов, то они описываются нелинейными дифференциальными уравнениями. Например, линейные электронные усилители при больших уровнях входных сигналов входят в насыщение. В то же время физические объекты при малых изменениях входных сигналов практически не проявляют нелинейных свойств и, поэтому, могут быть описаны линейными дифференциальными уравнениями. Операция замены нелинейного дифференциального уравнения приближённым линейным называется линеаризацией.
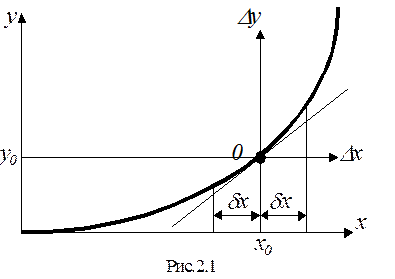
Основные моменты линеаризации (рис.2.1):
1. На графике нелинейной функции отмечается точка 0 начального режима - наиболее вероятная точка работы звена.
2. В этой точке проводится касательная и при малых отклонениях dx истинная кривая заменяется отрезком касательной прямой.
3. Вводится новая система координат - отклонения Dx и Dy. В этих координатах линеаризованное уравнение имеет нулевые начальные условия.
Техника линеаризации
Пусть имеется следующее дифференциальное уравнение, записанное в форме 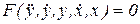 (2.1)
(2.1)
Тогда линеаризованное уравнение будет иметь вид:
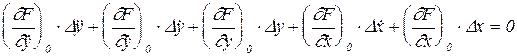 (2.2)
(2.2)
Рассмотрим более подробно технику линеаризации на примере.
Линеаризовать дифференциальное уравнение (ДУ)
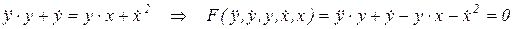 (2.3)
(2.3)
при начальных условиях:
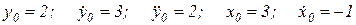 (2.4)
(2.4)
Проведем линеаризацию как указано выше:
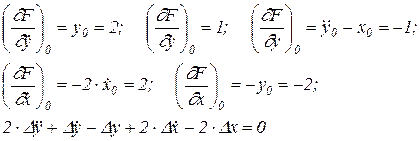 (2.5)
(2.5)
Далее будем использовать только линейные ДУ и потому знак D будем опускать:` 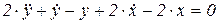 (2.6)
(2.6)
Уравнение (2.3) линеаризовано: оно заменяет исходное нелинейное дифференциальное уравнение в малой окрестности d около точки начальных условий.
Линейные ДУ могут быть записаны в естественной, символической и операторной формах.
Естественная форма:
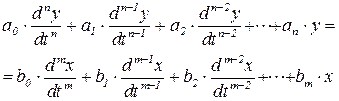 (2.7)
(2.7)
Если производная имеет порядок не выше 2-го, то можно использовать верхние точки в обозначениях производных: 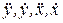 .
.
Символическая форма:
Производная n -го порядка заменяется символом
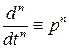 .
.
После замены уравнение (2.7) примет более простой вид:
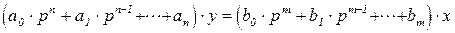 (2.8)
(2.8)
Уравнение, записанное в такой форме, можно преобразовывать как алгебраическое. Однако решение уравнение не упрощается.
Операторная форма:
В основе операторной формы записи уравнения лежит преобразование Лапласа: 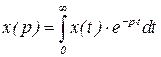 (2.9)
(2.9)
Если применить преобразование Лапласа к обеим частям дифференциального уравнения (2.7), то можно получить следующее операторное уравнение:
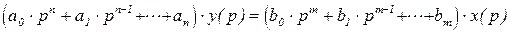 (2.10)
(2.10)
Следует обратить внимание на то, что значение p в операторной и символической формах совершенно различно – если в первой форме p является символом, и вводится исключительно для упрощения записи уравнения, то во втором – это комплексная переменная, введение которой влечет за собой простой подход к решению уравнения.
Операторная форма записи является основной формой, используемой в теории автоматического управления.
2.3. Передаточная функция
Учитывая то, что звенья описываются дифференциальными уравнениями, реальные сигналы заменяются их изображениями по Лапласу и дальнейшие расчеты ведутся в операторной форме.
 |
Передаточная функция W(p)– это отношение изображений выходного y(p) и входного x(p) сигналов при нулевых начальных условиях.
2.4. Таблица преобразований Лапласа
В ТАУ подавляющее большинство задач решается с использованием передаточной функции W(p) и нескольких простейших функций (табл.2.1)
Таблица 2.1
| Оригинал x(t) | Изображение x(p) | Название |
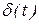 | 1 | Дельта-импульс |
| 1(t) | 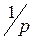 | Единичный сигнал |
| t | 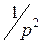 | Линейная функция |
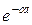 | 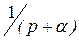 | Экспонента |
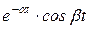 | 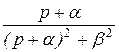 | Затухающие гармонические функции |
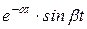 | 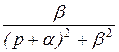 | Затухающие гармонические функции |
2.5. Типовые воздействия и реакции на них
Методы ТАУ позволяют рассчитать реакцию на любое входное воздействие, однако систематизированные результаты, обладающие некоторыми закономерностями, можно получить для ограниченного ряда входных сигналов. В качестве типовых входных сигналов рассматривают те, которые чаще всего встречаются на практике, а также в некотором смысле являются наиболее сложными для отработки их САУ.
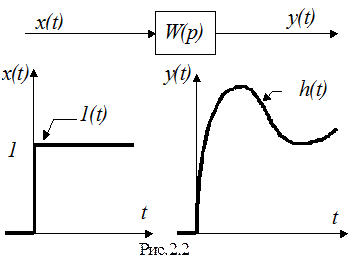 |
Реакция на единичный скачок 1(t) - переходной процесс h(t) (рис.2.2)
В электрических системах единичному скачку соответствует включение напряжения питания. Этот вид сигнала является для системы наиболее тяжелым для отработки. Если система отработает этот сигнал с заданными показателями качества, то наверняка будет качественно работать при других плавно изменяющихся сигналах.
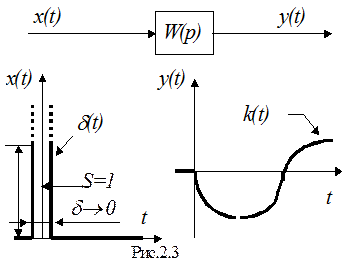 |
Реакция на дельта-импульс d(t) - функция веса k(t) (рис.2.3)
Дельта-импульс d(t) имеет нулевую длительность, бесконечную амплитуду и единичную площадь. Дельта-импульсу соответствует помеха в электрических схемах и удар в механических системах. Математический аппарат и свойства функции веса широко используется в расчётах импульсных САУ.
Реакция на гармонический сигнал - частотные характеристики (рис.2.4).
Если на вход линейной системы воздействует гармонический сигнал с амплитудой Xm и фазой jx, то на выходе будет сигнал той же частоты, однако другой амплитуды Ym и фазы jy.
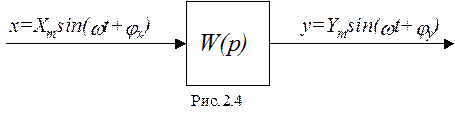 |
Изменения амплитуды Ym и фазы jy выходного сигнала y(t) зависят от частоты w входного сигнала x(t). Эти зависимости определятся следующие частотные характеристики: АЧХ (амплитудно-частотную) и ФЧХ (фазо-частотную):
АЧХ: 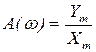 - коэффициент передачи (усиления) звена на данной частоте;
- коэффициент передачи (усиления) звена на данной частоте;
ФЧХ: 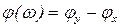 - сдвиг по фазе между выходным и входным сигналами.
- сдвиг по фазе между выходным и входным сигналами.
Частотные характеристики очень просто находятся при помощи передаточной функции.
3. Методы расчёта и построения графиков
переходных процессов и функции веса
Понятие переходного процесса является одним из важнейших понятий ТАУ, и особенно теории линейных систем. Поэтому умение легко, практически автоматически, рассчитывать функцию переходного процесса во многом определяет успех дальнейшего понимания ТАУ.
Как известно, передаточная функция звена – это отношение изображения по Лапласу выходного сигнала к изображению входного, которыми в частном случае могут быть переходный процесс h(p) и единичный сигнал 1(p)=1/p,
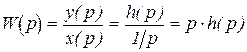 (3.1)
(3.1)
Из этого следует, что изображение переходного процесса

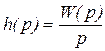 (3.2)
(3.2)
Аналогично для функции веса
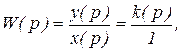 (3.3)
(3.3)
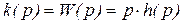 (3.4)
(3.4)
В соответствии со свойствами преобразования Лапласа, умножение изображения на p, соответствует однократному дифференцированию оригинала. Поэтому функция веса определяется также как производная от переходного процесса:
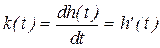 (3.5)
(3.5)
Заметим еще раз, что все функции комплексной переменной p - h(p), k(p) и т.д., являются изображениями соответствующих функций действительной переменной t - h(t), k(t) и т.д.
3.1. Примеры расчетов переходных процессов и функции веса
Далее расчёты переходного процесса, функции веса с построением их графиков выполним на числовых примерах.
Вид переходного процесса определяется корнями характеристического уравнения, образуемого приравниванием к нулю либо многочлена знаменателя передаточной функции, либо сомножителя при у(р) в операторном уравнении.
3.1.1.Корни характеристического уравнения действительные.
Пусть задано операторное уравнение САУ
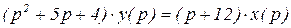 (3.6)
(3.6)
1. Разложение знаменателя на простейшие сомножители
Решаем характеристическое уравнение
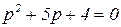 (3.7)
(3.7)
относительно p. Оно имеет следующие действительные корни:
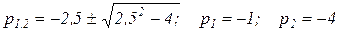 (3.8)
(3.8)
Следовательно, характеристический многочлен можно разложить на множители следующим способом:
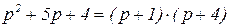 (3.9)
(3.9)
2.Определение оригинала табличным способом
Представляем выражение h(p) в виде суммы простейших дробей, оригиналы для каждой из которых имеются в таблице 2.1:
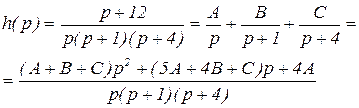 (3.10)
(3.10)
Чтобы коэффициенты при степенях p в левой и правой частях равенства (3.10) были бы одинаковыми, необходимо:
 . (3.11)
. (3.11)
Приравняв коэффициенты при одинаковых степенях p, получаем:
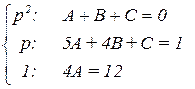 (3.12)
(3.12)
Решая, эту систему уравнений, получаем:
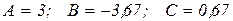 (3.13)
(3.13)
Окончательно получаем разложение h(p) на табличные выражения:
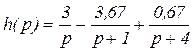 (3.14)
(3.14)
Перейдя согласно табл. 2.1 от изображений к оригиналам, получим:
 (3.15)
(3.15)
и для функции веса:
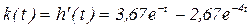 (3.16)
(3.16)
3. Построение графика переходного процесса
Для построения графика надо определить время счета и шаг изменения времени.
Определение времени счета:
Приводим выражение h(t) к стандартному виду, так что бы свободный член был равен 1: 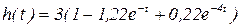 (3.17)
(3.17)
На бесконечности 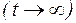 значение h(t) стремится к установившемуся значению hуст=3, так как обе экспоненты в выражении (3.17) обращаются в нуль.
значение h(t) стремится к установившемуся значению hуст=3, так как обе экспоненты в выражении (3.17) обращаются в нуль.
Находим время переходного процесса для каждой из экспонент.
Переходный процесс считается завершенным, когда его график h(t) попадает в 5%-зону установившегося значения, и далее не выходит из нее. В представлении переходного процесса в виде (3.17) установившееся значение для выражения, заключённого в скобки, равно 1. Поэтому время tпп1, в течение которого затухает 1-я экспонента, находится из уравнения
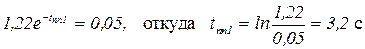 (3.18)
(3.18)
Аналогично находим время переходного процесса для 2-й экспоненты: 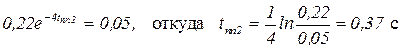 (3.19)
(3.19)
Время tпп всего переходного процесса не равно ни tпп1, ни tпп2, но меньше большего из этих двух значений. Точное значение tпп можно найти только из графика переходного процесса. Для аналитического его определения потребовалось бы решить трансцендентное уравнение, что невозможно.
Определение шага вычислений:
Шаг вычислений Dt выбираем таким образом, чтобы объём вычислений был минимальный и достаточный для построения графика. Здесь используется практическое правило: для построения гладкого графика вручную достаточно иметь 5-10 точек графика, через которые затем "на глаз" проводится весь график.
Согласно оценке (3.18) времени tпп1 для построения составляющей графика h(t), соответствующей 1-й экспоненте, шаг вычислений Dt1 должен быть равен 0,32...0,64 с. Аналогично, основываясь на оценке tпп2, находим Dt2= 0,04...0,08 с. Поэтому в интервале изменения t от 0 до 0,4 с вычисления ведём с шагом Dt1= 0,08 с, а далее до времени 3,2 с - с шагом Dt2= 0,4 с. Результаты вычислений сводятся в таблицу 3.1.
Таблица 3.1
| t | 0,08 | 0,16 | 0,24 | 0,32 | 0,4 | 0,8 | 1,2 | 1,6 | 2,4 | 2,8 | 3,2 | 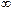 | ||
| h(t) | ||||||||||||||
| k(t) |
По данным этой таблицы строятся графики h(t) и k(t).
3.1.2.Корни характеристического уравнения комплексные
Этапы расчётов те же, что и в предыдущем примере, поэтому нумерацию этапов и названия далее не приводим.
Пусть задана передаточная функция
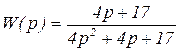 (3.20)
(3.20)
Решаем характеристическое уравнение
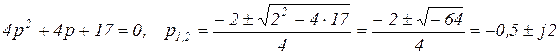 (3.21)
(3.21)
Корни комплексные, поэтому далее решение идет по другому пути.
Выделяем полный квадрат в знаменателе, а затем, как и раньше раскладываем выражение h(p) на сумму табличных выражений:
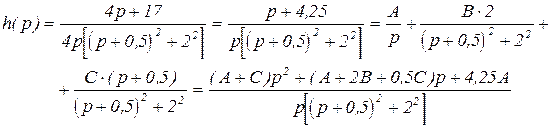 (3.22)
(3.22)
Равенство двух этих выражений дает нам систему уравнений для расчета значений коэффициентов А, В и С:

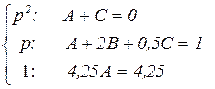 (3.23)
(3.23)
Решая, эту систему уравнений, получаем:
 (3.24)
(3.24)
Окончательно изображение переходного процесса примет вид:
 (3.25)
(3.25)
Переходим согласно табл.2.1 от изображений к оригиналам:
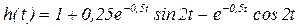 (3.26)
(3.26)
Далее находим функцию веса:
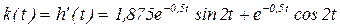 . (3.27)
. (3.27)
Определение времени счета:
Преобразуем данное выражение h(t) следующим образом:
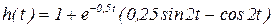 (3.28)
(3.28)
Сумму в скобке можно представить в виде одной функции sin:
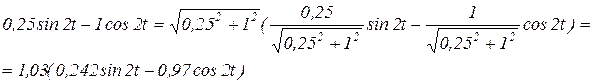 (3.29)
(3.29)
Мы имеем право на замену дробей 0,242 и 0,97 на cosg и sing, соответственно, т.к. сумма их квадратов равна 1: 0,2422+0,972=1. Это свойство коэффициентов при sinwt и coswt (в данном случае w=2) в выражении (3.29) верно всегда при выполнении преобразований, приведенных в этом выражении.
C учетом (3.29) h(t) можно представить в таком виде:
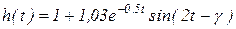 , (3.30)
, (3.30)
где 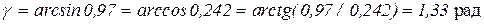 (вычислить g можно по любой формуле из приведенного их ряда).
(вычислить g можно по любой формуле из приведенного их ряда).
Окончательно:
 (3.31)
(3.31)
Так как функция sin по модулю не превосходит 1, то время переходного процесса можно вычислить так же, как и раньше, из уравнения:
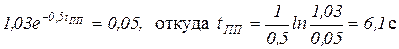 (3.32)
(3.32)
График переходного процесса колебательный и будет содержать экстремальные точки. Для их нахождения используется производная от h(t), т.е. функция веса k(t):
 k(t)=0, 1,875e-0,5tsin2t+e-0,5tcos2t=0, tg2t=-1/1,875=-0,533,
k(t)=0, 1,875e-0,5tsin2t+e-0,5tcos2t=0, tg2t=-1/1,875=-0,533,
откуда
te=(arctg(-0,533)+pn)/2=-0,245+pn/2 (рад), где n=1,2,3...
Значения te: te1= 1,325 c, te2= 2,9 c; te3= 4,465 c, te4= 6,03 c и т.д.
Определение шага вычислений:
Из времени tпп =6,1 с находим шаг вычислений Dt= 1с; Время t =0..7.
Далее заполняется таблица (табл.3.2) вычислений при найденных значениях t и затем строятся графики h(t) и k(t).
| t | 1,325 | 2,9 | 3,7 | 4,465 | 6,03 | ∞ | ||||
| h(t) | ||||||||||
| k(t) |
4.Частотные характеристики линейных САУ
Частотные характеристики линейных САУ рассчитываются через передаточные функции: если W(p) – передаточная функция, то W(jw) – частотная характеристика (ЧХ), получаемая из передаточной функции путём замены в ней p на jw.
ЧХ как комплексное число может быть представлено в показательной и алгебраической формах.
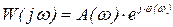 (4.1)
(4.1)
Эта запись позволяет найти еще две важнейшие характеристики: АЧХ и ФЧХ:
A(w) – амплитудо-частотная характеристика (АЧХ);
j(w) – фазо-частотная характеристика (ФЧХ).
Алгебраическая форма:
W(jw)=P(w)+jQ(w) (4.2)
 |
Данное выражение порождает еще две характеристики: 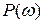 – вещественно-частотная характеристика (ВЧХ)и
– вещественно-частотная характеристика (ВЧХ)и 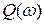 – мнимо-частотная характеристика (МЧХ).
– мнимо-частотная характеристика (МЧХ).
График ЧХ на комплексной плоскости называется годографом (рис.4.1). Между величинами A, j, P и Q существуют связи (аргумент w опущен):
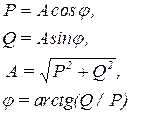 (4.3)
(4.3)
Особенности вычислений ЧХ можно проследить только на числовом примере.
Пусть передаточная функция звена имеет вид
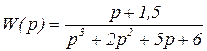 (4.4)
(4.4)
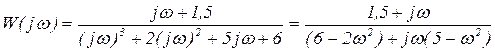 (4.5)
(4.5)
 2014-02-02
2014-02-02 1982
1982







