Тема: Общие направления развития ТАУ. 2 страница

Формально в записи (4.5) ЧХ представляет собой отношение двух комплексных чисел числителя и знаменателя. Далее вычисляем:

* АЧХ: 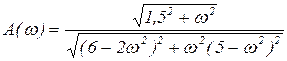(4.6)

* ФЧХ: (4.7)

* ВЧХ и МЧХ домножением числителя и знаменателя ЧХ на комплексно-сопряженное к знаменателю число:

откуда

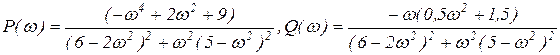(4.8)

Как видно, вывод выражений A(w), j(w), P(w) и Q(w) принципиально прост. Сложным являются вычисления с целью построения годографа ЧХ, если принять во внимание, что при этих вычислениях нужно знать, до какого значения аргумента w нужно считать (полный интервал изменения w от 0 до ¥) и каким должен быть шаг Dw вычислений? В сравнении с расчётами переходных процессов расчёты ЧХ сложнее тем, что нет простых процедур определения конечной (верхней) частоты w счёта и шага Dw, который к тому же будет неравномерным.

Здесь следует пользоваться проверенными на практике приёмами расчёта ЧХ:

1. Необходимо предугадать вчерне вид годографа, а именно, где его начало и конец, через какие квадранты комплексной плоскости и в каком порядке он пройдёт при изменении частоты w от 0 до ¥.

Прежде всего находят точки пересечения годографа с осями координат. Для этого решают уравнения:

P(w)=0 Þ -w⁴+2w²+9=0 Þ w=2,04, т.е. годограф пересекает мнимую ось на частоте w₄=2,04, если в качестве иллюстрации расчётов принять рис.4.1;

Q(w)=0 Þ w(0,5w²+1,5)=0 Þ w=0, т.е. годограф пересекает действительную (вещественную) ось на частоте w₁=0.

Далее вычисляют значения P(w) и Q(w) при найденных частотах и на бесконечности при w=¥.

2. Определяют значение угла j(¥), с которым годограф входит в начало координат, по формуле

j(¥)=-90^o(n-m), (4.9)

где n и m - степени полиномов p, соответственно, знаменателя и числителя передаточной функции.

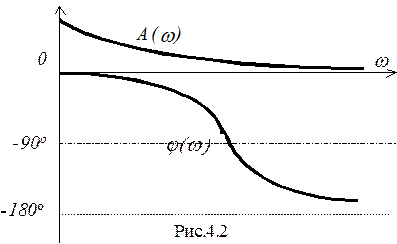
По результатам описанных вычислений строится в черновом варианте годограф ЧХ (рис.4.1).

3. Подготавливается таблица вычислений, состоящая из 5-ти строк (табл.4.1)

Таблица 4.1

w	w1=0	w2	w3	w4=2,04	w5	w6	w7	w=¥
P(w)
Q(w)
A(w)
j(w)				-90o				-180o

В этой таблице прежде всего нужно заполнить первую строку - строку частот w. Все остальные строки затем заполнятся вычислениями по формулам (4.6)...(4.8).

Сначала находим частоты w₂ и w₃ для точек годографа, лежащих в 4-м квадранте. Очевидно, что эти частоты должны быть такими, чтобы точки годографа на этих частотах равномерно заполняли бы участок в 4-м квадранте, т.е. угол j между соседними точками был примерно равен 30^о (ни в коем случае не надо стремиться получить точно 30^о, а лучше задать, например, 30^о10^о). Руководствуясь этими соображениями, задаёмся частотой в пределах от 0 до 2,04 (эти значения верны только для рассматриваемого числового примера!) и вычисляем угол j. Если он равен 30^о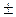10^о, то нами найдена (точнее - угадана) частота w₂. Если вычисления дали 60^о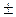10^о, то найдена частота w₃. Иначе нужно снова задать значение w. Аналогично определяют частоты w₅...w₇ для 3-го квадранта.

После заполнения строки частот заполняется значениями вся таблица. По значениям P(w) и Q(w) строится годограф W(jw) (рис.4.1), а по значениям A(w) и j(w) строятся АЧХ и ФЧХ (рис.4.2).

Замечание к расчётам по формуле (4.7) значений угла j на калькуляторе, компьютере и по таблицам тригонометрических функций. Во всех перечисленных случаях определяется только главные значения арктангенса - ARCTG(*), - которые находятся в пределах от -90^о до +90^о. Действительное значение угла определяется с учётом структуры выражения, находящегося под знаком arctg, которое является отношением мнимой Q к действительной P части соответствующего комплексного числа. Если P>0, то угол лежит в 1-м или 4-м квадрантах, если P<0, то угол лежит во 2-м или 3-м квадрантах. При Р=0 угол равен 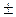90^о:

arctg(Q/Р)= 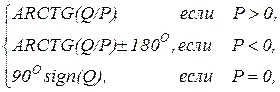(4.10)

где sign(Q) - знак числа Q.

Как видно из приведенных выше приёмов расчёта ЧХ такой расчёт содержит достаточно сложные вычисления.

Из частотных характеристик в ТАУ чаще всего используются асимптотические логарифмические амплитудно-частотные характеристики (ЛАЧХ). Преимущество ЛАЧХ в том, что их расчёт чрезвычайно прост при достаточно высокой точности. При использовании ЛАЧХ проблем с длительным выбором (угадыва-нием) частот, при которых следует выполнять вычисления, не существует.

5. Типовые звенья САУ

Звенья САУ могут иметь передаточную функцию с полиномами числителя и знаменателя произвольного порядка

(5.1)

Из курса алгебры известно, что полиномы любой степени могут быть представлены в виде произведения выражений типа

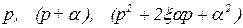(5.2)

Тогда передаточная функция может быть представлена в виде произведения и частного таких выражений. Звенья, передаточная функция которых содержит кроме постоянных чисел только не более двух выражений типа (5.2) в числителе или знаменателе, называют типовыми или элементарными звеньями.

Типовые звенья подразделяются на позиционные, интегрирующие и дифференцирующие. Позиционные звенья имеют для установившегося режима статические характеристики вида y=kx, аинтегрирующие и дифференцирующие таких характеристик не имеют.

Виды типовых позиционных звеньев:

1. Безинерционное (пропорциональное) звено имеет передаточную функцию и описыватся алгебраическим уравнением, соответственно, вида

W(p)=k, y=kx (5.3)

Примерами безинерционных звеньев служат рычажная передача (рис.5.1а), потенциометрический датчик перемещения (рис.5.1б).

В этих звеньях выходной сигнал у повторяет без задержки по форме входной сигнал х.

2. Апериодическое (инерционное) звено 1-го порядка имеет передаточную функцию и описывается уравнением вида

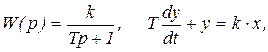(5.4)

где k, Т - коэффициент передачи и постоянная времени звена.

Примерами этого звена служат сервопривод, охваченный жесткой обратной связью (см. рис.18.1), судовой дизель без регулятора (рис.22.1), холодильная камера (рис.5.2а).

Переходный процесс описывается выражением

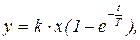(5.5)

где вместо x=1(t), как должно быть для переходного процесса, принято фактическое значение сигнала x, благодаря чему рассчитывается реакция звена на скачок произвольной величины.

График переходного процесса приведён на рис.5.2б. Установившееся значение y_уст, равное kx, достигается на бесконечности: t®¥. Время переходного процесса t_пп, определяемое по моменту окончательного вхождения графика в 5% зону допуска от у_уст, составляет 3T. Звено обладает самовыравниванием. Свойство самовыравнивания состоит в том, что звено самостоятельно без применения дополнительного регулирования приходит к постоянному по величине установившемуся значению.

3. Инерционное звено 2-го порядка имеет передаточную функцию (5.6)

Особенность звена в том, что его характеристическое уравнение имеет действительные корни.

Примером этого звена служит центробежный датчик скорости (рис.10.1) при большой силе F_Г гидравлического трения.

Переходный процесс описывается выражением

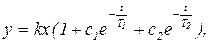(5.7)

где с₁ и с₂ - постоянные интегрирования.

График переходного процесса (рис.5.3а) имеет точку перегиба. Время переходного процесса можно определить только графически.

4. Колебательное звено имеет передаточную функцию

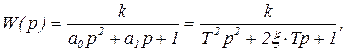(5.8)

где T - период свободных (незатухающих) колебаний;

x - параметр затухания, принимающий значения 0<x<1.

Особенность звена в том, что его характеристическое уравнение имеет комплексно сопряженные корни.

Примером этого звена служит центробежный датчик скорости (рис.10.1) при малой силе F_Г гидравлического трения.

Переходный процесс описывается выражением

(5.9)

где - резонансная частота с учётом затухания колебаний.

График переходного процесса приведён на рис.5.3б.

Виды типовых интегрирующих звеньев:

1. Идеальное интегрирующее звено имеет передаточную функцию и дифференциальное уравнение

(5.10)

где k - коэффициент размерности, равный отношению размерностей выходного и входного сигналов;

T - постоянная времени интегрирующего звена, определяющая скорость изменения выходного сигнала.

Примером данного звена является простой гидравлический сервопривод (рис.17.1).

Переходный процесс описывается выражением

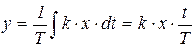(5.11)

и имеет графиком прямую линию (рис.5.4а).

Интегрирующее звено не имеет установившегося значения и, поэтому, самовыравниванием не обладает и не имеет статической характеристики.

2. Инерционное интегрирующее звено имеет передаточную функцию и дифференциальное уравнение

(5.12)

Примером инерционного интегрирующего звена является судно (рис.29.1), если входным сигналом считать угол поворота руля, а выходным - курс судна. Переходный процесс звена описывается выражением

(5.13)

и имеет график, приведённый на рис.5.4б.

3. Изодромное звено имеет передаточную функцию и дифференциальное уравнение

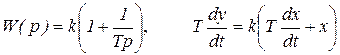(5.14)

Примером изодромного звена является упруго присоединённый катаркт (рис.5.5а), если входным сигналом считать силу F, а выходным - перемещение точки приложения этой силы.

Переходный процесс описывается выражением

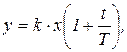(5.15)

а график приведён на рис.5.5б.

Виды типовых дифференцирующих звеньев:

1. Идеальное дифференцирующее звено имеет передаточную функцию и описывается дифференциальным уравнением

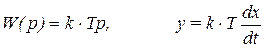(5.16)

Примером идеального дифференцирующего звена можно считать электрический датчик частоты вращения (тахометр), если входным его сигналом считать угол a поворота вала ротора, а выходным - снимаемое с якоря напряжение u (рис.5.6а). При этом моментом инерции датчика нужно пренебречь.

Переходный процесс для идеального дифференцирующего звена имеет вид дельта-импульса d(t), который физически нереализуем. Для его реализации потребовалось бы скачкообразное (мгновенное) изменение углового положения ротора, для чего потребовалось бы приложить к ротору бесконечно большую силу, что невозможно. Поэтому график переходного процесса для идеального дифференцирующего звена не строится.

2. Инерционное (реальное) дифференцирующее звено имеет передаточную функцию и дифференциальное уравнение

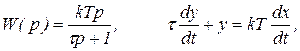причём (5.17)

Примером этого типа звена является датчик скорости (рис.5.6а), в котором учтена инерционность ротора. Также инерционным дифференцирующим звеном является гидравлический демпфер (рис.5.6б), если входным сигналом х считать перемещение поршня, а выходным у - перемещение цилиндра.

Переходный процесс описывается выражением

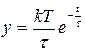(5.18)

и имеет график, приведённый на рис.5.6в.

Все дифференцирующие звенья обладают самовыравниванием, но не имеют статической характеристики, так как различным по величине входным сигналам x в установившемся режиме соответствует одно и то же значение выходного сигнала у=0.

6.Структурные схемы САУ и их преобразования

В САУ, как видно из рис.1.1, входят различные элементы, каждый из которых имеет свою передаточную функцию. Соединение звеньев между собой, изображенных в виде прямоугольников с обозначением в них передаточных функций звеньев, называется структурной схемой САУ (рис.6.1 и т.д.). Со структурными схемами проводятся различные преобразования, среди которых основным является сворачивание структурной схемы в одно звено с эквивалентной передаточной функцией W_{экв .} Существуют 3 типовых схемы соединения звеньев, который сворачиваются в одно звено за один приём без каких-либо дополнительных преобразований. Это - последовательное, параллельное соединения и соединение с обратной связью.

Последовательное соединение на примере 3-х звеньев изображено на рис.6.1а. На линиях связи между звеньями не должно быть ни точек ветвления, ни точек слияния. Звенья друг относительно друга могут располагаться на чертеже под любым углом, могут располагаться также встречно, главное их связи между собой. Эквивалентная передаточная функция равна

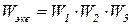(6.1)

Вывод этой формулы достаточно прост

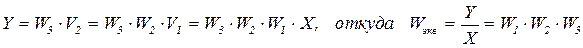(6.2)

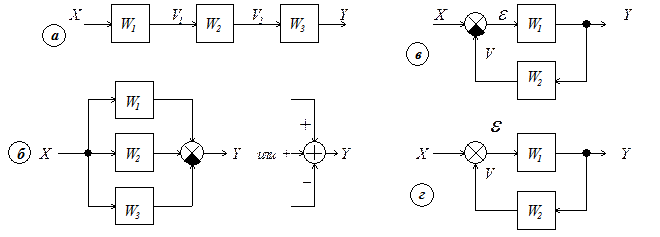Рис.6.1

Параллельное соединение на примере 3-х звеньев изображено на рис.6.1б. Главным в этом соединении звеньев является то, что все они имеют один и тот же входной сигнал, а выходные сигналы звеньев должны суммироваться алгебраически на элементе - сумматоре. Варианты изображения сумматора сигналов показаны на рисунке, причём в варианте с секторами затемняется сектор, в котором сигнал является вычитаемым. Эквивалентная передаточная функция равна

(6.3)

Соединения с обратной связью на примерах отрицательной обратной связи (сигнал, пропорциональный выходному сигналу, вычитается из входного сигнала) и положительной обратной связи (сигнал, пропорциональный выходному сигналу, складывается с входным сигналом) изображены, соответственно, на рис.6.1в и рис.6.1г.

Эквивалентная передаточная функция равна

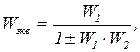(6.4)

где знак "+" при отрицательной, а знак "-" при положительной обратной связи.

Для соединения с отрицательной обратной связью вывод формулы (6.4) следующий. Согласно схемы рис.6.1в составим выражение

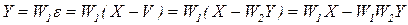(6.5)

Из него находим отношение Y/X, которое будет равно W_экв согласно (6.4).

Если структурная схема не содержит рассмотренных типовых соединений, то их нужно создавать путём структурных преобразований.

В структурных схемах имеются объекты трёх видов: изображения звеньев, точки ветвления и точки слияния (суммирования/вычитания).

Рис.6.2

Имеется 4 вида структурных преобразований, позволяющих решить подавляющее число задач сворачивания структурной схемы:

1. Преобразования точек ветвления согласно рис.6.2а.

2. Преобразования точек слияния согласно рис.6.2б.

При этих преобразованиях количество звеньев структурной схемы не изменяется.

3. Переносы точки ветвления по цепи звеньев вперёд или назад согласно рис.6.2в.

4. Переносы точки слияния по цепи звеньев вперёд или назад согласно рис.6.2г.

При этих переносах точек ветвления и слияния в схему добавляется одно новое звено. Передаточная функция дополнительного звена должна быть такой, чтобы ни один выходной сигнал преобразованной структурной схемы не изменился. Это правило отражено на рис.6.2в и рис.6.2г.

Пример сворачивания структурной схемы приведён на рис.6.3.

Исходная схема а (рис.6.3а) не имеет типовых соединений звеньев. Схема б получена из схемы а переносом назад по цепи элементов W₂ и W₃ точки ветвления 4. Добавлено звено W₃. Схема в получена из схемы б заменой соединения с обратной связью звеном W₄. Схема г получена из схемы в заменой последовательно соединенных и охваченных единичной обратной связью звеньев W₁ и W₄ одним звеном W₅. Схема д - конечная.

Далее приводим вычисления передаточных функций эквивалентных звеньев участков и схемы в целом.

Переход от б к в:

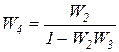
Переход от в к г:

Переход от г к д:

Рис.6.3

7. Устойчивость линейных САУ.

Определение допустимых настроек САУ

Под устойчивостью линейной САУ понимают свойство затухания переходного процесса при t®¥, т.е. переходный процесс имеет установившееся значение.

Учитывая то, что в линейных САУ по существу рассматриваются линеаризованные системы, то указанный вид устойчивости справедлив при малых отклонениях от первоначального устойчивого состояния. Эту устойчивость называют также "устойчивостью в малом". Иллюстрации такой устойчивости приведены на рис.7.1.

Для дизеля, центробежного датчика частоты вращения вычисляют показатель - фактор устойчивости - см. (11.5), (21.2).

Свойство устойчивости для САУ является обязательным, так как неустойчивая САУ фактически неработоспособна.

Свойство устойчивости может быть определено по графику переходного процесса (рис.7.1г). Однако расчёт и построение графика переходного процесса требует больших вычислений. Проще установить устойчивость без построения графика h(t), а только по корням характеристического уравнения изображения переходного процесса h(p). Каждому корню характеристического уравнения соответствует свой член, входящий как слагаемое в выражение h(t) переходного процесса. Таблица такого соответствия для распространённых случаев имеет вид:

Таблица 7.1

Тип корня характеристического уравнения	Член в h(t)	Переходный процесс
1. p=0	С	Устойчив
2. p1=0, p2=0 (два нулевых корня)	С×t	Неустойчив
3. p=a (действительный корень)		Устойчив при a<0 и неустойчив при a>0
4. p=a±jb (комплексные корни)		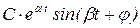Устойчив при a<0 и неустойчив при a>0
5. p=±jb (корни чисто мнимые)		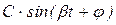На грани устойчивости

Оценка устойчивости либо по графику переходного процесса, либо по корням характеристического уравнения имеет тот недостаток, что её невозможно в общем случае применить к САУ, в передаточной функции которой содержится хотя бы один буквенный коэффициент, так как не существует аналитических методов решения алгебраических уравнений (именно таким уравнением является характеристическое уравнение САУ) выше 3-й степени. По этой же причине неприменима указанная оценка устойчивости на этапе синтеза САУ.

В ТАУ для оценки устойчивости применяются критерии устойчивости. Критериями устойчивости называются совокупность процедур, с помощью которых можно установить факт устойчивости САУ без нахождения корней характеристического уравнения. Существуют различные виды таких критериев как алгебраических, так и частотных. Ниже рассмотрены критерии Гурвица и Найквиста.

Критерий Гурвица алгебраический. Для оценки устойчивости используется характеристический многочлен передаточной функции замкнутой САУ. Структура САУ может быть любой.

Пусть замкнутая САУ имеет следующую передаточную функцию

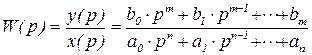(7.1)

Из коэффициентов характеристического многочлена

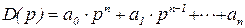(7.2)

составляем следующую матрицу

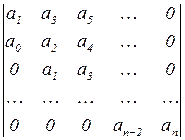(7.3)

Порядок заполнения матрицы следующий. Сначала по диагонали матрицы располагают коэффициенты от a₁ до a_n. Затем над диагональными элементами располагают коэффициенты с возрастающими индексами. Если коэффициенты в процессе заполнения все исчерпаны, то ставят 0. Далее под диагональными элементами располагают коэффициенты с убывающими индексами. Если коэффициенты в процессе заполнения все исчерпаны, то ставят 0.

Формулировка критерия Гурвица: САУ устойчива, если все коэффициенты характеристического многочлена положительны и положительны все n главных (диагональных) определителей Гурвица матрицы (7.3):

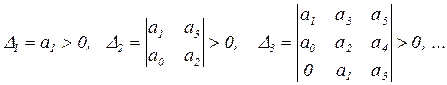(7.4)

Последний определитель не вычисляют, так как его знак совпадает со знаком D_n-1:

D_n=a_n×D_n-1 (7.5)

Если хотя бы один определитель Гурвица отрицателен, то САУ неустойчива. Если имеется хотя бы один определитель Гурвица равен нулю при остальных положительных, то САУ находится на границе устойчивости.

Числовой пример.

Определить устойчивость САУ с передаточной функцией

(7.6)

Составляем матрицу Гурвица и главные определители

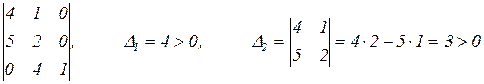(7.7)

Оба определителя положительны, поэтому САУ устойчива.

Если передаточная функция САУ содержит хотя бы один буквенный коэффициент, значение которого может быть любым числом, то с помощью критерия Гурвица можно определить допустимые по условию устойчивости значения такого коэффициента. При двух буквенных коэффициентах возможно совместное определение допустимых значений таких коэффициентов и выделение областей устойчивости на плоскости этих коэффициентов. Покажем это на примере.

Пусть САУ управления курсом судна, представленная на рис.7.2, состоит из двух звеньев - авторулевого и судна. Передаточные функции авторулевого и судна имеют вид, соответственно,

(7.8)

Параметром настройки авторулевого является коэффициент передачи K. Постоянная времени T судна изменяется от 10 с при порожнем судне до 60 с при полностью загруженном. Необходимо найти такие значения параметра K, при которых САУ устойчива при изменении загрузки судна.

Определяем передаточную функцию замкнутой САУ

(7.9)

Составляем матрицу Гурвица и вычисляем 2-й определитель:

(7.10)

С учётом положительности всех коэффициентов характеристического многочлена при условии (7.10) САУ будет устойчива при одновременном выполнении следующей системы неравенств

(7.11)

САУ будет находиться на границе устойчивости, если будет выполнено хотя бы одно из равенств

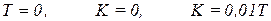. (7.12)

Другие два неравенства должны быть типа (7.11).

Каждое из равенств (7.12) является на плоскости T-K границей области устойчивости (рис.7.3). Штриховкой обозначены области устойчивости по отношению к линиям границы устойчивости. Общая область a0d для всех заштрихованных областей является областью устойчивости САУ.