Тема: Общие направления развития ТАУ. 6 страница

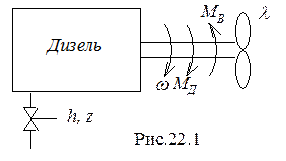
Дизель (рис.22.1), сжигая поступающее в него топливо, развивает механический момент М_Д и вращает винт с частотой w. Винт оказывает дизелю момент сопротивления М_В. Величина момента М_В зависит от величины разворота l лопастей. Момент и частота вращения дизеля зависит от величины подачи топлива, которая регулируется перемещением h рейки топливного насоса. Если дизель оборудован автоматическим регулятором частоты вращения, то подача топлива определяется величиной перемещения z муфты центробежного датчика скорости.

Уравнение динамики ГД имеет вид

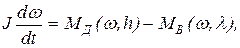(22.1)

где J - момент инерции ГД.

Зависимости М_Д(w,h) и M_B(w,l) от величин w, h и l в общем случае нелинейные, поэтому дифференциальное уравнение (22.1) также нелинейное. Основным режимом работы ГД является поддержание постоянства частоты вращения w винта. При этом за счёт возмущений могут кратковременно изменяться в небольших пределах частота вращения w, моменты М_Д и М_В, разворот l лопастей винта и параметры h и z. При указанных малых изменениях дифференциальное уравнение (22.1) можно заменить линеаризованным, причём будет также мала погрешность описания динамических процессов ГД. Замена нелинейного дифференциального уравнения (22.1) приближенным линейным упростит анализ динамических процессов в ГД при достаточной точности расчетов.

Если обозначить через w₀, М_Д0, М_В0, l₀, h₀ и z₀ начальные значения параметров работы ГД, а через Dw, DМ_Д, DМ_В, Dl, Dh и Dz величины отклонений w, М_Д, М_В, l, h и z от начальных значений, то линеаризованное уравнение будет иметь вид

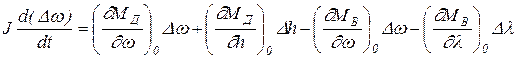(22.2)

Введем обозначения производной символом р и фактора устойчивости F_Д (21.2) и преобразуем (22.2) к виду

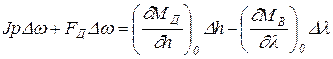(22.3)

Делим обе части (22.3) на F_Д

(22.4)

Вводим обозначения

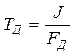- постоянная времени ГД;

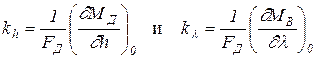- коэффициенты передачи ГД, соответственно, по управлению (перемещению h рейки топливного насоса) и возмущению (развороту l лопастей винта).

Окончательно операторное уравнение ГД примет вид

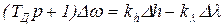(22.5)

Из (22.5) сигнал Dw определится выражением

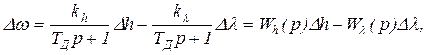(22.6)

где 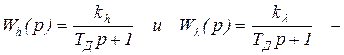(22.7)

передаточные функции ГД, соответственно, по управлению и по возмущению.

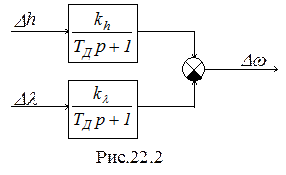
Структурная схема ГД как элемента САУ в соответствии с (22.6) приведена на рис.22.2.

Если входным управляющим сигналом служит перемещение z муфты центробежного датчика скорости, то для получения зависимости Dw=f(Dz, Dl) необходимо в уравнении (22.5) выполнить замену

(22.8)

где производная (dh/dz)₀ определяется из графической зависимости между h и z (рис.22.3), которую можно рассчитать для ГД, который оборудован системой автоматического регулирования частоты вращения. График h=f(z) должен быть падающим, так как в САУ частотой вращения ГД должно быть так, чтобы при увеличении частоты вращения w и соответствующем этому увеличении перемещения z муфты центробежного датчика скорости, подача топлива должна быть уменьшена. Подача же топлива пропорциональна перемещению h топливной рейки.

После подстановки (22.8) в (22.5) получим

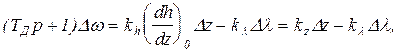(22.9)

где k_z - коэффициент передачи по управлению от датчика скорости, причём k_z<0.

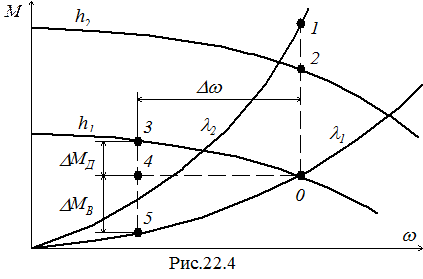
Значения частных производных, входящих в уравнение (22.2), через которые затем вычисляются постоянная времени и коэффициенты передачи ГД определяются из графиков статических характеристик дизеля и винта (рис.22.4).

Пусть начальная точка 0. Для определения частных производных по частоте даём приращение Dw частоте w. На графике механической характеристики дизеля этому приращению будет соответствовать точка 3, а на графике винтовой характеристики будет соответствовать точка 5. Изменения моментов дизеля и винта при этом приращении будут составлять DM_Д и DM_В. Частные производные приближенно равны

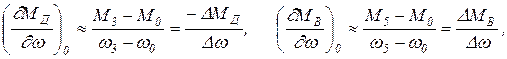(22.10)

где обозначено M_i - значение момента в i -й точке.

Далее при постоянной частоте вращения, равной w₀, изменяем значение положения топливной рейки от h₁ до h₂. Этому изменению h соответствует переход в точку 2. Приближенно

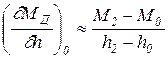(22.11)

Если при постоянной частоте вращения изменить разворот лопастей винта от значения l₁ до l₂, то будет получена точка 1, и приближённо

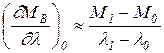(22.12)

23. Переходный процесс ГД без регулятора

Регистром флота определяется совокупность показателей качества работы судовых дизелей как ГД, так дизель-генераторных агрегатов:

Для главных двигателей:

· неравномерность регулирования частоты вращения, определяемая в диапазоне изменения нагрузки на ГД в пределах от холостого хода до номинального момента как

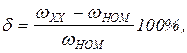(23.1)

где w_XX - частота вращения холостого хода, w_HOM - номинальная частота вращения, причем для однодвигательного агрегата должно быть d£12%, а для двухдвигательных агрегатов - d£3%;

· для ГД, входящего в систему дистанционного автоматического управления (ДАУ ГД) должно быть d<1,5%;

· статическая ошибка регулирования частоты вращения не более 2%;

· заброс частоты в переходном процессе не более 10%;

· время переходного процесса t_ПП не выше 10 с;

· ограничения по частоте вращения в диапазоне 30...115%.

В дополнение к регуляторам частоты вращения ГД должны иметь отдельные предельные выключатели при частоте вращения выше номинальной на 20%.

Для дизель-генераторов:

· наклон регуляторной характеристики или неравномерность регулирования частоты не более 5%;

· статическая ошибка регулирования частоты вращения не более 1%;

· заброс частоты в переходном процессе не более 10%;

· время переходного процесса t_ПП не выше 5 с;

· предельный выключатель на 115% номинальной частота вращения.

Рассмотрим возможности выполнения указанных показателей качества для ГД, не оборудованных автоматикой регулирования частоты вращения.

В соответствии с выражениями (22.6), (22.7) и структурной схемой ГД, приведённой на рис.22.2, передаточные функции по сигналам управления Dh и возмущения Dl являются одинаковыми по типу и представляют собой апериодические звенья первого порядка. Переходные процессы для частоты Dw при изменении либо Dh, либо Dl также будут подобны друг другу. Поэтому для анализа достаточно рассчитать переходный процесс Dw только, например, при изменении Dh положения топливной рейки, т.е. при условиях Dh¹0 и Dl=0.

Из (22.6) при Dh¹0 и Dl=0 имеем

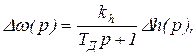(23.2)

где подчеркнуто записями Dw(p) и Dh(p) то, что они являются изображениями по Лапласу от величин Dw и Dh.

При скачкообразном изменении Dh, которому соответствует изображение по Лапласу вида Dh(p)=Dh/p (табл.2.1), изображение переходного процесса для Dw(p) будет следующим

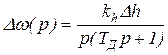(23.3)

Вид переходного процесса будет зависеть от значения постоянной времени Т_Д, которая определяется через фактор устойчивости F_Д выражением

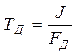(23.4)

Переходный процесс при условии, что Т_Д¹0 согласно (5.5) будет следующим 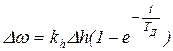(23.5)

Если Т_Д=0, что соответствует бесконечно большому значению фактора устойчивости F_Д=¥, переходный процесс будет безинерционным

Dw=k_hDh (23.6)

Если Т_Д=¥, что соответствует условию F_Д=0, то операторное уравнение ГД, полученное из (22.3) и передаточная функция будут иметь вид

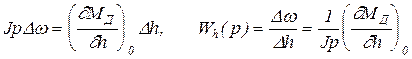(23.7)

Передаточная функция (23.7) соответствует интегрирующему звену и согласно (5.11) переходный процесс будет следующим

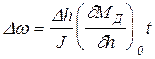(23.8)

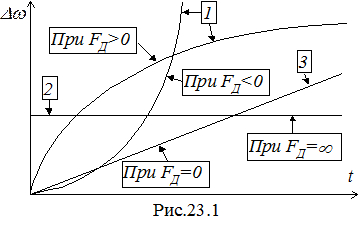
По выражениям (23.5), (23.6) и (23.8) построены на рис.23.1 графики переходных процессов, соответственно, 1, 2 и 3.

Видно, что при отрицательном и нулевом значениях фактора устойчивости F_Д ГД неустойчив. При положительном значении F_Д ГД устойчив, причём с уменьшением F_Д время переходного процесса возрастает. Для ГД, применяемых на судах, время переходного процесса лежит в пределах 45...100 с, что намного превышает допустимое по Регистру. Неравномерность d частоты вращения и отклонение частоты вращения от заданной также намного превышают значения, определённые Регистром. Следовательно ГД без регулятора частоты вращения практически неработоспособен.

Исправить положение можно, если при отклонениях частоты вращения от заданной изменять подачу топлива, воздействуя на рейку топливного насоса.

В принципе при положительном и достаточно большом по величине значении фактора устойчивости F_Д такое регулирование может выполняться вручную обслуживающим персоналом. Однако это утомительно для персонала, зависит от субъективных их способностей, что не гарантирует постоянного поддержания требуемых показателей качества регулирования. При отрицательном факторе устойчивости F_Д, а также при быстро меняющихся процессах ручное регулирование вообще непригодно.

24. Структурная схема САУ ГД с регулятором прямого действия. Уравнение узла с датчиком скорости

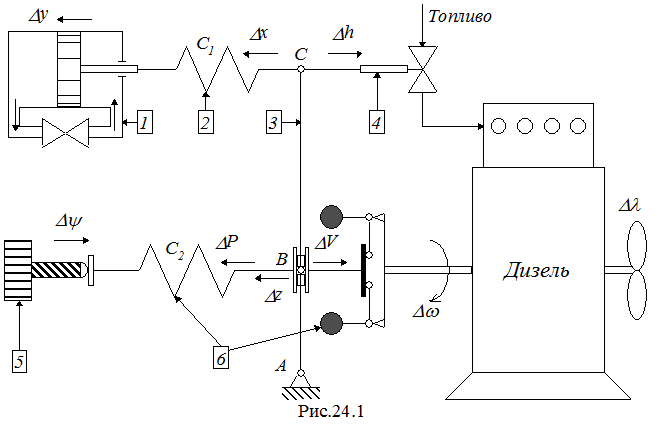
Структурная схема САУ ГД с регулятором прямого действия приведена на рис.24.1. На схеме обозначено:

· 1 - катаракт; 2 - пружина катаракта; 3 - рычаг; 4 -топливная рейка; 5 - винт задатчика частоты вращения; 6 - датчик скорости;

· С₁ и С₂ - жесткости пружин катаракта и датчика скорости;

· Dy, Dх - перемещения поршня и правого конца пружины катаракта;

· Dh - перемещение топливной реки (при указанном на рисунке перемещении рейки подача топлива возрастает);

· Dy - перемещение винта задатчика частоты вращения (при указанном на рисунке перемещении величина заданной частоты вращения увеличивается);

· Dz - перемещение муфты центробежного датчика скорости (указанное на рисунке направление перемещения соответствует увеличению частоты вращения);

· Dw и Dl - изменения частоты вращения и разворота лопастей винта;

· DP и DV - изменения поддерживающей и восстанавливающей сил.

Работает САУ следующим образом. Пусть при уменьшении разворота l лопастей винта частота вращения w увеличилась. Тогда муфта датчика скорости 6 сместится влево. Вместе с муфтой влево сместится точка В рычага 3, и рычаг повернётся против часовой стрелки. Смещение влево точки С рычага, а вместе с ней и смещение влево топливной рейки 4 уменьшит подачу топлива, что приведёт к снижению частоты вращения w.

Для демпфирования (подавления) скачкообразного изменения подачи топлива при резком изменении частоты вращения дизеля применяют катаракт 1, подсоединенный к рейке через пружину 2 (такое подключение катаракта называют упругим). При резком возрастании частоты вращения резко возрастает поддерживающая сила DP датчика 6, а восстанавливающая сила DV в начале изменения частоты вращения создаётся сразу двумя пружинами - катаракта и датчика. Этим ограничивается первоначальное перемещение топливной рейки. Далее сжатая пружина 2 перемещает поршень катаракта 1 влево, причем скорость перемещения поршня зависит от сечения вентиля, через который соединяются правая и левая полости цилиндра катаракта. По мере смещения поршня катаракта влево сила сжатия пружины 2 уменьшается, что приводит к дополнительному смещению топливной рейки влево. Так как перемещение поршня катаракта растянуто по времени, то и перемещение топливной рейки происходит также плавно.

Поворотом ручки задатчика частоты вращения головка винта 5, например, смещается вправо, пружина датчика скорости дополнительно сжимается, точка В смещается вправо и через рычаг 3 и топливную рейку 4 увеличивается подача топлива. Частота вращения w дизеля увеличивается.

Полное описание САУ ГД будет состоять из дифференциальных уравнений дизеля, дифференциального уравнения датчика скорости с учётом упруго присоединенного катаракта и самого катаракта.

Для вывода уравнения динамики датчика скорости с учётом упруго присоединённого катаракта воспользуемся ранее выведенным выражением (11.3) 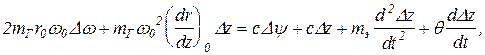заменив в нём члены cDy+cDz, входящие в выражение изменения восстанавливающей силы DV.

На точку В непосредственно действует сила сжатия пружины датчика, которую обозначим как N₁ и которая определяется точно также, как и в (11.1):

N₁=c₂Dy+c₂Dz (24.1)

На точку С действует сила сжатия, равная

c₁Dx-c₁Dy (24.2)

Если обозначить передаточное число рычага как

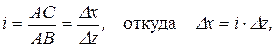(24.3)

то на точку В будет также действовать сила от сжатия пружины 2, определяемая как N₂=i(c₁Dx-c₁Dy)=i(c₁iDz-c₁Dy)=c₁i²Dz-ic₁Dy (24.4)

Полная сила упругости пружин, приведенная к точке В, равна

N=N₁+N₂=c₂Dy+c₂Dz+ c₁i²Dz-ic₁Dy=c₂Dy+(c₂+ c₁i²)Dz-ic₁Dy (24.5)

Заменив cDy+cDz в (11.3) на N, получим

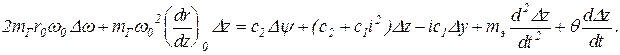(24.6)

Преобразуем, введя обозначение производной символом р,

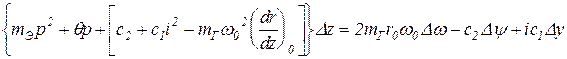(24.7)

Введем обозначение фактора устойчивости регулятора

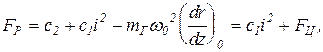(24.8)

где F_Ц - фактор устойчивости центробежного датчика скорости согласно (11.5).

Поделив на (24.8) обе части уравнения (24.7), получим

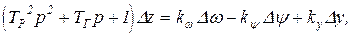(24.9)

где 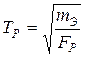- инерционная постоянная времени регулятора;

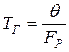- постоянная времени гидравлического трения;

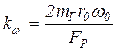- коэффициент передачи регулятора по частоте вращения;

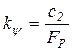- коэффициент передачи регулятора по сигналу задания;

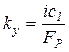- коэффициент передачи регулятора по сигналу катаракта.

По любому из входных сигналов Dw, Dy и Dy датчик скорости в составе САУ представляет собой динамическое звено 2-го порядка.

Из рисунка найдём используемую при расчёте (22.8) производную

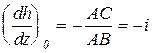(24.10)

25. Полная система уравнений ГД

с регулятором прямого действия

Для САУ ГД с регулятором прямого действия, структурная схема которой приведена на рис.24.1, необходимо составить дифференциальные уравнения дизеля и упруго присоединённого катаракта 1.

Входными сигналами дизеля по схеме являются величины изменений подачи топлива Dh и разворота Dl лопастей винта. Выходной сигнал - изменение частоты вращения Dw дизеля. Это полностью совпадает с обозначениями сигналов дизеля, приведённых на рис.22.1. Поэтому воспользуемся готовым дифференциальным уравнением дизеля в виде (22.9):

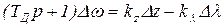(25.1)

На поршень катаракта 1 справа налево действует сила сжатия пружины, определяемая выражением (24.2). С учётом соотношения (24.3) указанная сила определится выражением

c₁(iDz-Dy) (25.2)

Слева направо на поршень действует сила гидравлического сопротивления, которая создаётся разностью давлений по обе стороны поршня. Под действием этой разности давлений масло протекает через вентиль, соединяющий правую и левую полости цилиндра. Сила сопротивления пропорциональна скорости протекания масла через вентиль. Если учесть несжимаемость масла, то скорость протекания масла через вентиль будет прямо пропорциональна скорости движения поршня. Следовательно, сила гидравлического сопротивления определится как

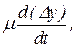(25.3)

где m - коэффициент гидравлического сопротивления вентиля, зависящий от его проходного сечения, причём m обратно пропорционально указанному сечению.

Приравняв между собой (25.2) и (25.3), получим дифференциальное уравнение катаракта

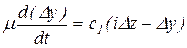(25.4)

Вводим обозначение производной символом р и преобразуем (25.4)

(25.5)

где Т_К - постоянная времени катаракта.

Полная система дифференциальных уравнений ГД, оборудованного регулятором частоты вращения прямого действия, имеет вид

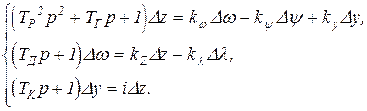(25.6)

В этой системе из трёх уравнений содержится три переменных Dz, Dw и Dy, зависящие от двух сигналов Dy и Dl. В принципе эта система разрешима относительно любой зависимой переменной Dz, Dw и Dy. Дифференциальное уравнение по каждой переменной Dz, Dw и Dy будет иметь производные до 4-го порядка, и, поэтому, САУ ГД описывается дифференциальным уравнением 4-го порядка.

Аналитически дифференциальные уравнения 4-го порядка не решаются. Поэтому рассчитать в общем виде переходный процесс невозможно. Однако можно проводить исследование САУ по критериям устойчивости, при применении которых не требуется искать решение дифференциального уравнения. Возможно также определение ошибок регулирования, так как они находятся по формуле (8.2) также без необходимости решения дифференциального уравнения.

26. Расчёт регуляторной характеристики ГД

Регуляторная характеристика (РХ) определяется для установившихся режимов как зависимость изменения частоты вращения ГД от изменения нагрузки на валу ГД. Поэтому РХ нужно рассчитывать по уравнениям установившегося режима, которые получаются из системы дифференциальных уравнений (25.6) при р=0,

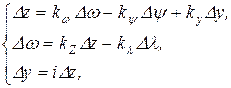(26.1)

дополнив её выражением изменения момента на валу ГД. Например, при линеаризации винтовой характеристики M=M_B(w,l) получим

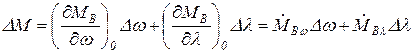(26.2)

При расчёте РХ задание частоты вращения не должно изменяться, поэтому принимаем Dy=0.

Упруго присоединённый катаракт действует на топливную рейку и, следовательно, оказывает влияние на систему только в переходных режимах. Поэтому в расчётах РХ катаракт не должен учитываться, что достигается двумя способами. Так третье уравнение системы (26.1) описывает только катаракт, и его далее в расчетах не учитываем. Если принять жесткость с₁ пружины катаракта равной нулю, то это будет эквивалентно тому, что катаракт отключен от рейки 3 (рис.24.1) регулятора частоты вращения и, следовательно, не учитывается в работе регулятора. Условие c₁=0 эквивалентно условию k_y=0 (см. обозначения к (24.9)).

Отбросив в (26.1) третье уравнение, приняв Dy=0 и k_y=0 и учтя (26.2) получим систему уравнений, которую будем использовать при расчёте РХ

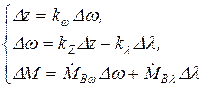(26.3)

Исключаем из (26.3) сначала Dz

а затем исключаем Dl

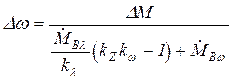(26.4)

Используем ранее вычисленные величины (при с₁=0):

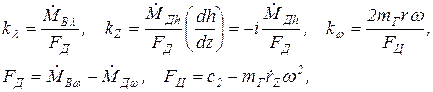(26.5)

где для упрощения записи применено обозначение производных "точкой сверху" и опущен индекс 0 начальных условий у соответствующих переменных.

Преобразуем знаменатель выражения (26.4)

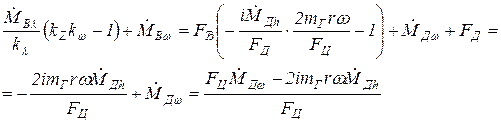(26.6)

Подставляем (26.6) в (26.4), получаем выражение регуляторной характеристики

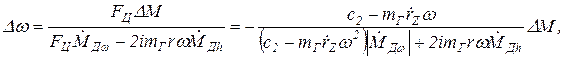(26.7)

где учтено то, что всегда 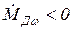и .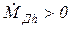

По выражению (26.7) можно исследовать влияние параметров и характеристик всех элементов САУ на форму РХ. Исследуем влияние части параметров.

1. Влияние коэффициента передачи i рычага.

Так как коэффициент i входит в знаменатель выражения РХ (26.7), то при увеличении i изменение частоты Dw всегда уменьшается.

2. Влияние жесткости с₂ пружины центробежного датчика скорости.

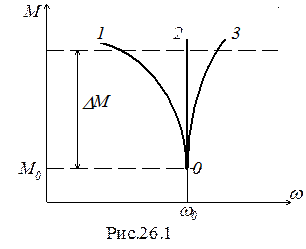
Если пока не учитывать влияния на Dw частоты вращения w или принять небольшие пределы изменения частоты w, то (рис.26.1):

· при жёсткой пружине (с₂ велико) фактор устойчивости F_Ц датчика больше нуля и дробь перед DM в выражении (26.7) всегда отрицательная и, следовательно при увеличении момента M нагрузки частота вращения будет падать (линия 1);

· при мягкой пружине (с₂ мало) фактор устойчивости F_Ц датчика меньше нуля и если F_Ц мало по абсолютной величине, то дробь перед DM в выражении (26.7) положительная и, следовательно при увеличении момента M нагрузки частота вращения будет расти (линия 3); очевидно, что такая форма РХ неприемлема в практике;

· при оптимальной жесткости пружины, когда 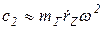, частота вращения w практически не зависит от момента нагрузки М (линия 2).

3. Влияние частоты вращения w.

В САУ ГД обычно применяют датчик скорости с жёсткой пружиной. Это объясняется тем, что при мягкой пружине при прочих равных условиях выше вероятность потери устойчивости системы. Поэтому во всём рабочем диапазоне частот от холостого хода w_xx до максимально допустимой 1,15w_ном фактор устойчивости 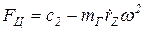положителен.

В соответствии с (26.7) при увеличении w числитель уменьшается. В знаменателе находится сумма двух членов. Первый член 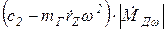при увеличении w уменьшается. Второй член 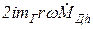при увеличении w увеличивается. При параметрах ГД и элементов регулятора в существующих САУ ГД значение знаменателя в целом возрастает при увеличении частоты w. Следовательно, с увеличением частоты w значение дроби, стоящей перед DM в выражении (26.7), по абсолютной величине уменьшается, т.е. с увеличением частоты вращения w чувствительность её к изменению момента нагрузки падает. График 1 для этого случая имеет характерный изгиб.

Выводы по расчётам регуляторной характеристики:

Уменьшить изменение Dw частоты вращения при изменении нагрузки ГД или уменьшить неравномерность d РХ можно путём оптимального уменьшения жесткости пружины центробежного датчика скорости и увеличением коэффициента передачи рычага регулятора.

27. Анализ устойчивости САУ ГД

с регулятором прямого действия

Исследованием на устойчивость устанавливается влияние на неё характеристик дизеля, винта, датчика скорости, катаракта, рычага. Для исследования применим критерий устойчивости Гурвица. Если исходить из системы уравнений САУ ГД в виде (25.6), то характеристическое уравнение САУ будет 4-го порядка. Исследование с помощью критерия Гурвица будет довольно громоздким. Если учесть реально существующие соотношения между постоянными времени элементов САУ

Т_р<T_Г<<Т_К<Т_Д, (27.1)

то в первом приближении можно пренебречь очень малыми постоянными времени Т_р и T_Г, приняв их равными нулю, и исследовать устойчивость САУ ГД по упрощенной системе уравнений, вытекающих при названных допущениях из (25.6),

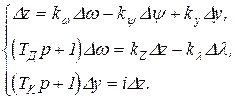(27.2)

В этой системе уравнений входных сигналов два: Dl и Dy, а выходных - три: Dz, Dw и Dy. Для линейных САУ свойство устойчивости не зависит от вида и величины входных сигналов. Это важное положение обосновывается довольно просто. Так, например, при исследовании устойчивости по критерию Гурвица используется характеристический многочлен (7.2) передаточной функции замкнутой САУ. Характеристический же многочлен, как следует из (7.1), представляет собой многочлен, на который умножается только выходной сигнал САУ, но не входные сигналы. Поэтому можно принять Dl=0 и Dy=0, и система (27.2) преобразуется в более простую для анализа устойчивости систему