САР напряжения генератора постоянного тока

Для примера рассмотрим схему САР напряжения генератора постоянного тока (рис.37).

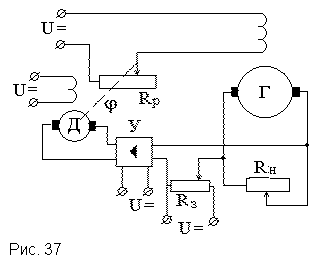
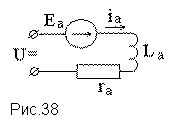
Выведем дифференциальное уравнение исполнительного двигателя постоянного тока. Его схема замещения изображена на рис. 38.

Для якорной цепи справедливо уравнение

Если принять, что 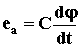, гдеj 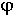– угол поворота вала двигателя, то

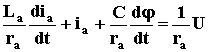то есть

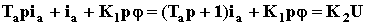где 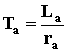– постоянная времени якорной цепи; 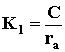, 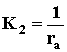– коэффициенты пропорциональнсти.

Если учесть, что 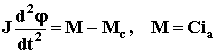, где J – момент инерции якоря, M - электромагнитный момент, М_с – момент сторонних сил, то получим

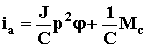Следовательно

= >

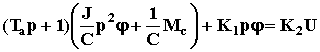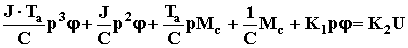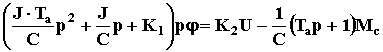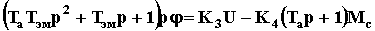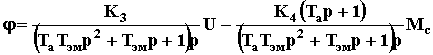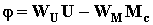Здесь 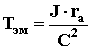– электромеханическая постоянная времени;

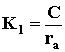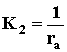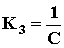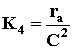; ; ; – коэффициенты пропорциональности;

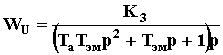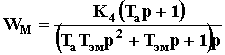, – передаточные функции по напряжению и моменту сторонних сил.

Структурная схема двигателя постоянного тока показана на рис.39.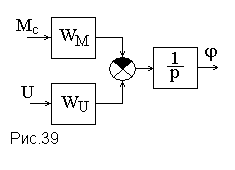

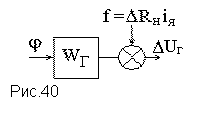
Аналогичным образом выводится передаточная функция генератора постоянного тока, которая с учетом пренебрежения индуктивностью обмотки якоря имеет вид, показанный на рис.40, где

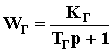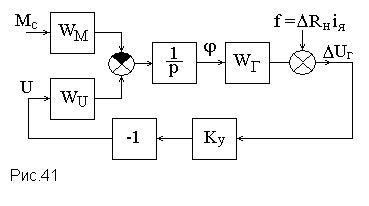
Усилитель можно представить пропорциональным звеном с коэффициентом усиления K _у. В окончательном виде структурная схема САР напряжения генератора постоянного тока показана на рис.41.