Частотный спектр лазерного резонатора

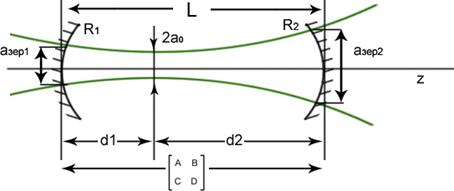
Алгебра резонатора

Связывает параметры резонатора с параметрами Гауссова пучка.

Комплексный параметр гауссова пучка:

, =,

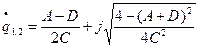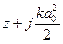Используя правила знаков, получаем: d1=-z1, z1=

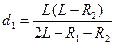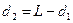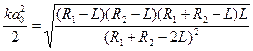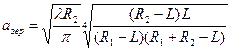1. Частотный спектр лазерного резонатора вытекает из условия баланса фаз.

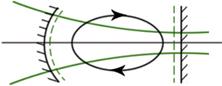
Для линейного резонатора:

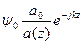
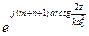
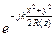
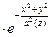
Фаза гауссова пучка: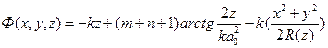

Один проход кратен π. Ф(z₁)-Ф(z₂)=qπ, |z₂-z₁|=L (длина резонатора)

Ф(0,0,z)=-k_mnz+(m+n+1)arctg(2z/k_mna₀²)

k_mn=2πν_mn/c

-k(z₁-z₂)+(m+n+1)[arctg(2z₁/ ka₀²)-arctg(2z₂/ ka₀²)]= qπ

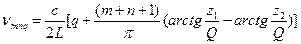, где Q=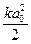- конфокальный параметр.

Воспользовавшись тригонометрическими формулами разницы arctg, преобразованием arctg=>arccos, получаем:

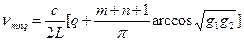- каноническая форма частоты для моды.

Формула содержит в себе критерий устойчивости: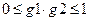

Пусть m=n=0 (волна типа 00)

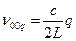
Частотный спектр – это множество (дискретный ряд) собственных частот мод резонатора.

Мода – это тип колебания в резонаторе. Моды бывают продольные и поперечные.

1. Продольная мода:

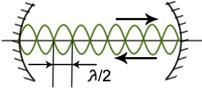
Условие устойчивости - 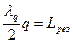, , 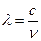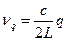-продольный тип колебаний.

2. Поперечная мода: ТЕМmn

Т.о. мода-объемная структура поля в резонаторе. Она определяется индексами поперечной моды m, n и индексом продольной моды q. (это определяет волны в резонаторе.)

Мода:

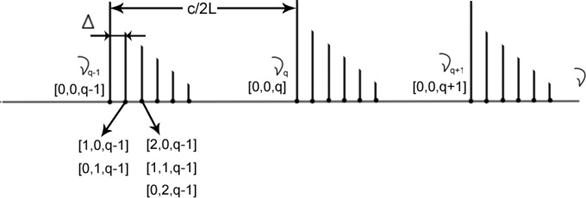
Чем выше порядок поперечных колебаний, тем ниже добротность контура (большие потери)

Чтобы частоты были вечественными, необходимо выполнение условия 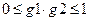(см. диаграмму устойчивости)

Если 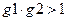, то 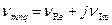, 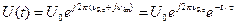- затухания (дифракционные потери)