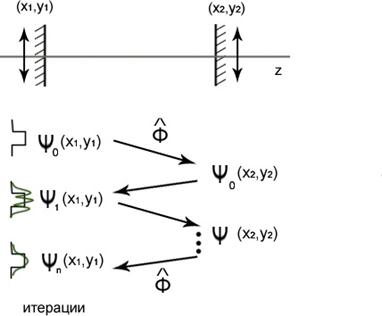
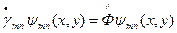 - Задача на собственные функции (моды
- Задача на собственные функции (моды 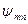 ) и собственные значения (
) и собственные значения (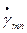 ) для интегрального оператора Френеля
) для интегрального оператора Френеля 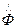 .
.
Это интегральное уравнение 1-го рода, путь решения- итерационный, при котором начальное значение распределение может быть теоретически произвольным (моды формируются в процессе генерации)
Физический смысл 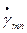 = |
= |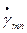 |е-j arg
|е-j arg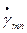
1) |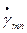 | - отвечает за изменение амплитуды, 1-|
| - отвечает за изменение амплитуды, 1-|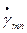 |2 – определяет дифракционные потери.
|2 – определяет дифракционные потери.
2) arg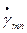 отвечает за дополнительный сдвиг фаз, который приобретает волна (дополнительные фазовые набеги, обусловленные дифракцией)
отвечает за дополнительный сдвиг фаз, который приобретает волна (дополнительные фазовые набеги, обусловленные дифракцией)
Это влияет на баланс фаз, на частотный спектр.
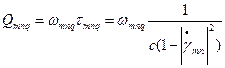 ,
, 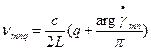
Существенные параметры резонатора:
1) Частотный спектр {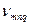 }
}
2) Потери в резонаторе { α.пот mnq., Qmnq, τmnq}
Резонатор формирует каустику пуска- распределение поля в резонаторе и за его пределами.
Геометрические параметры распределения поля: {a(z1), a(z2), ka02/2, d1, d2, Θрасх}
Резонатор характеризуется: {R1, R2, L, rотр1, rотр2, a1,a2}
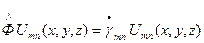 ,
, 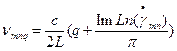
g1=1-R1/L, g2=1-R2/L
обобщенные параметры: G1=g1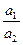 , G2=g2
, G2=g2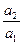
обобщенные параметры координат: X1=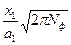 , X2=
, X2=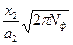
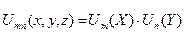 - независимые распределения.
- независимые распределения.
Обобщенное дифракционное уравнение резонатора:
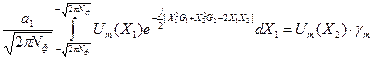
Частный случай:
1. Конфокальный резонатор G1=0=G2, Nф>>1
Такое интегральное уравнение может быть решено точно:
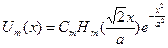 - гауссов пучок.
- гауссов пучок.
Если число Френеля конечное Nф<1 - уравнение имеет другое решение. Полученное решение относится к конфокальному резонатору только при условии, что Nф>>1.
При конечных значениях числа Френеля исходное уравнение:
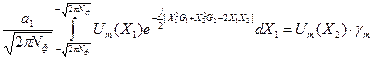
принимает вид:
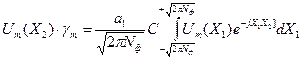
Это уравнение имеет точное решение в виде специальных функций – сфероидальных вытянутых угловых функций и вытянутых радиальных функций.
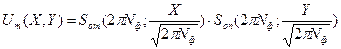 - распределение поля на зеркалах.
- распределение поля на зеркалах.
Собственные числа 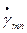 :
:
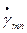 =
=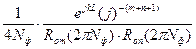 (отвечает за амплитуду и дополнительную фазу)
(отвечает за амплитуду и дополнительную фазу)
Где 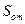 ,
, 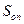 - сфероидальные вытянутые угловые функции,
- сфероидальные вытянутые угловые функции, 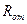 ,
, 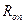 - вытянутые радиальные функции (ф-я Ламера).
- вытянутые радиальные функции (ф-я Ламера).
Графики: (номограммы)
Для иллюстрации решения резонатора рассмотрим график распределения поля на зеркале резонатора для двух числе Френеля.
(результат точного оптического расчета)
Мода TEM00
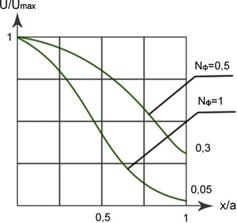
x/a=1- край зеркала.
Вывод:
Увеличение числа Френеля приводит к резкому уменьшению амплитуды поля на краю зеркала, что резко уменьшает дифракционные потери. Это распределение похоже на ТЕМ00
Единственный резонатор, решаемый точно- это конфокальный.
Мода TEM01
Рассмотрим распределение поля на апертуре зеркала для моды 01.
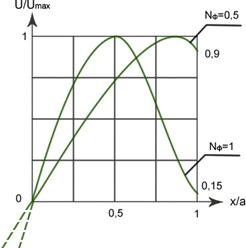
1. Если увеличивается число Френеля- поле на краю зеркала резко уменьшается
2. Сопоставляя графики приходим к выводу- у мод высшего порядка дифракционные потери больше, чем для мод 00
 2014-02-03
2014-02-03 810
810

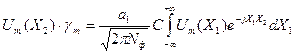 -
-






