Рассмотрим частные случаи

1. Пластинка λ/4, 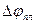=π/2

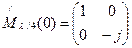- матрица пластинки в собственных осях.

2. Пластинка λ/2, 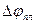= π

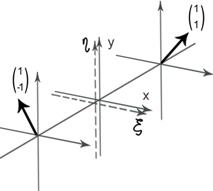
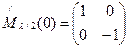
При прохождении световой волны через данную пластинку на выходе получается ортогональная поляризация

Пример: правокруговая поляризация переходит в левокруговую:

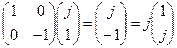
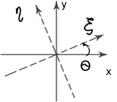
Произвольный угол между ξ и х

Матрица фазовой пластинки с произвольным радиусом:

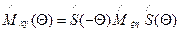
Можно показать, что:

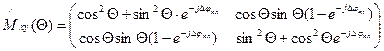
Фазовая пластинка- это фазовый поляризационный элемент.

Поляризатор- это амплитудный поляризационный элемент.

Запишем матрицу произвольного поляризационного элемента в собственных осях (диагональная матрица):

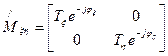
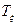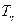У идеального поляризатора =1, =0

Вывод:

Любой поляризационно-анизотропный элемент имеет 2 собственные оси:

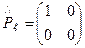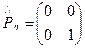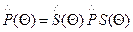, , , где Θ-угол между ξ и х.

=

=

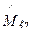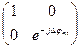
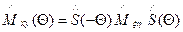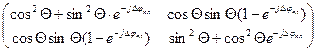
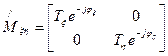
Комплексное число z=|z|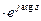=|z|(cos(argz)+jsin(argz))