Определение: Под векторным произведением двух векторов 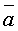 и
и 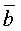 понимается вектор,
понимается вектор,  для которого:
для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е. 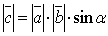 , где
, где 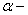 угол между векторами
угол между векторами 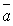 и
и 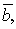
-этот вектор перпендикулярен перемножаемым векторам, т.е. 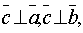
-если векторы 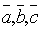 неколлинеарны, то они образуют правую тройку векторов.
неколлинеарны, то они образуют правую тройку векторов.
Свойства векторного произведения:
1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е. 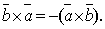
2. Векторный квадрат равен нуль-вектору, т.е. 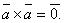
3. Скалярный множитель можно выносить за знак векторного произведения, т.е. 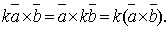
4. Для любых трех векторов 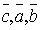 справедливо равенство
справедливо равенство 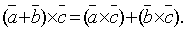
5. Необходимое и достаточное условие коллинеарности двух векторов 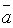 и
и 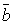 :
: 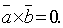
 2014-02-03
2014-02-03 627
627








