Раздел 3. Основные понятия и методы

     Раздел 3. Основные понятия и методы

дифференциального и интегрального исчисления

План лекции:

1. Задачи, приводящие к понятию «производная».

2. Приращение аргумента и функции.

3. Производная.

4. Нахождение производной функции.

5. Правила и формулы дифференцирования.

6. Производная сложной функции.

 

При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.

Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И.Ньютона и Г.Лейбница.

Механическое истолкование производной было впервые дано И.Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени.

Лейбниц пришел к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной уравнением.

Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к ее траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на ее орбите сводится к определению направления касательной к кривой.

Определение сложному понятию «производная» мы будем давать на основании понятия более простого «Приращение функции».

 

 

    Часто нас интересует не значение какой – либо величины, а ее изменение. Например, сила упругости пружины пропорциональна удлинению пружины; работа есть изменение энергии; средняя скорость – это отношение перемещения к промежутку времени, за который было совершено перемещение, и т. д.

Пусть дан график функции у= f(x).

Рассмотрим точку М₀ с абсциссой x_o. Пусть ∆х – это изменение абсциссы от точки x_o до х, т.е. ∆х = х – x_o , M₀М – секущая, M₀N – касательная.

        

    Рассмотрим две такие задачи.

Задача 1. Пусть дан график функции у= f(x).

Рассмотрим точку М₀ с абсциссой x_o. Пусть ∆х – это изменение абсциссы от точки x_o до х, т.е. ∆х = х – x_o , M₀М – секущая, M₀N – касательная.

 

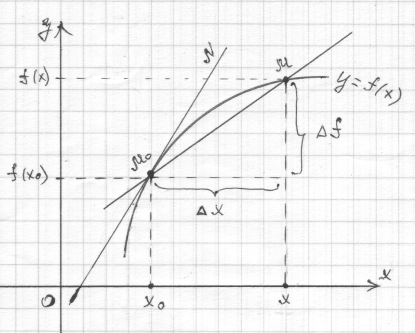
Найдем:

а) угловой коэффициент секущей (это средняя скорость изменения функции);

б) угловой коэффициент касательной (подсказка: касательная – это предельное положение секущей)

Решение: у= f(x) – заданная функция, ∆х = х – x_o – изменениеабсциссы от точки x_o до х.

v_ср = 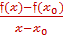. В нашем случае k_сек =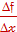

При х→х₀ (или ∆х →0)будет f(x)→f(x₀), следовательно, M₀М→ M₀N.

Тогда k _асс =  .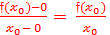

Задача 2. Рассмотрим движение материальной точки М по прямой с выбранным на ней началом отсчета – точкой О. Расстояние от начала отсчета до точки М в каждый момент времени t обозначим буквой s. Тогда движение точки М будет описываться функцией

s = s (t), t[ t₀; t ].

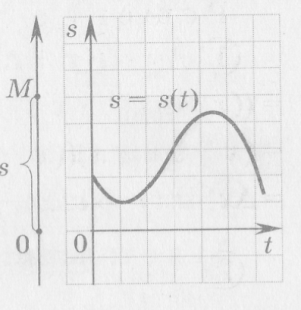
Найдем:

а) среднюю скорость за отрезок [ t₀; t ];

б) скорость точки в момент времени t₀ (мгновенную скорость).

Решение: За промежуток времени длительности t – t₀ между моментами времени t₀ и t точка проходит путь равный s (t) –s(t₀).

Среднюю скорость получают, разделив перемещение материальной точки s на изменение времени, в течение которого оно совершено.

Тогда v_ср =  ;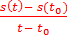

Чем меньше рассматриваемый промежуток времени, тем точнее можно охарактеризовать движение. А мгновенной скоростью называется число, к которому стремится разностное отношение средней скорости за промежуток времени от t₀ до t при t→ t_0.

Тогда v_мгн =  .

Подобные задачи рассматриваются и в экономике, и в анализе ценовой политики. Например: «цена товара напрямую зависит от расходов на производство» или «объем реализации некоторой продукции зависит от роста или снижения его цены».

А теперь давайте подведём итоги нашей исследовательской работы. Вы решали различные задачи, но все они привели к одной и той же математической модели: к числу, к которому стремиться отношение разности значений функции к разности значений аргумента. В русском языке для величины, на которую изменилось начальное количество, используется слово «прирост».