Правила и формулы дифференцирования
Итак, мы уже знаем три формулы для нахождения производных:
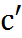 = 0 (хn)' = nxn-1 x1 = 1
= 0 (хn)' = nxn-1 x1 = 1
Пользуясь этими формулами и вспомогательными формулами действий над степенями из школьного курса.
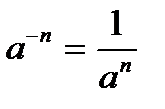 и
и  ,
,
выведем формулы для нахождения производных функций 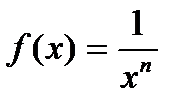 и
и 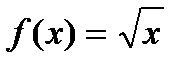
1) 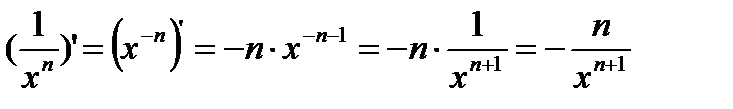
Получили формулу 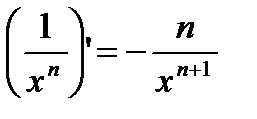 (*)
(*)
Пример. 1) 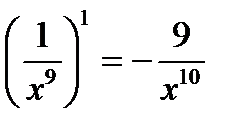
2) 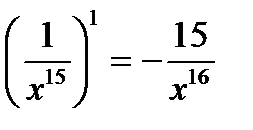
из формулы (*) следует формула 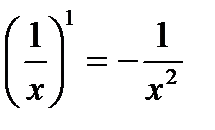
Найдем производную функции f(x)= 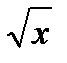
Будем использовать формулы:
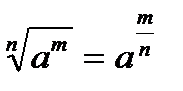
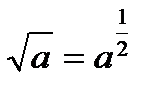
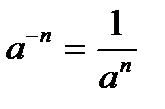
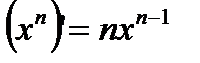
Итак, получили новую формулу: производная корня квадратного имеет вид 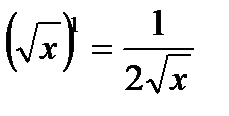
Правила и формулы дифференцирования следует обязательно знать, чтобы не повторять каждый раз все выкладки при нахождении данной функции. Ведь существует бесконечное множество функций и с их усложнением непосредственное дифференцирование становится все более трудоемким.
Формулы дифференцирования
| C ' =0, | 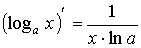
|
| x ' =1, | 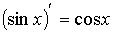
|
| (кх + b)' = к, где к и b – x числа | 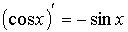
|
| (хn)' = nxn-1 | 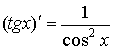
|
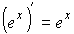
| 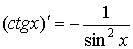
|
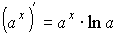
| 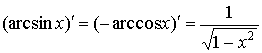
|
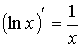
| 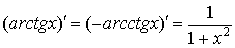
|
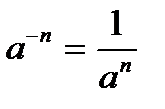
| 
|
В таблице представлены основные формулы нахождения производных функций.
Разберем несколько примеров на нахождение производных функций с помощь. Формул, указанных в таблице.
Пример 1. Найти производную функции y = x4
Р е ш е н и е: Имеем y' = (x4)' = 4x3
Пример 2. Найти производную функции y = 3cos(x)
Р е ш е н и е: Имеем y' = (3cos(x))' = -3sin(x)
Пример 3. Найти производную функции y = tg (x)
Р е ш е н и е: Имеем 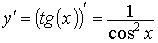
Пример 4. Найти производную функции y = arcsin (x)
Р е ш е н и е: Имеем 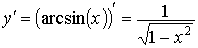
 2022-01-07
2022-01-07 339
339








