Основные правила дифференцирования
I. Производная суммы (разности):
(u+v)' =u' + v',
Пример1. Найти производную функции y = sin(x) + x3
Р е ш е н и е:
Имеем y' = (sin(x) + x3)' = cos(x) + 3x2
Постоянный множитель выносится за знак производной
(Cu)' =C u',
II. Производная произведения
Пусть функция представляет собой произведения двух функций u и υ.
(читается: u - y υ-вэ).
(u·υ)' = u'·υ+u·υ'
Пример 1
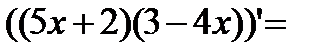
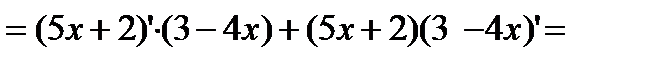
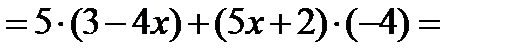
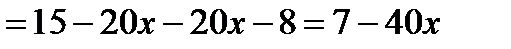
Пример 2.
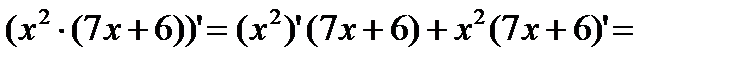
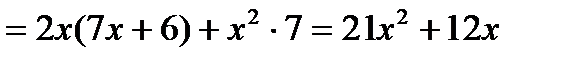
III. Производная дроби
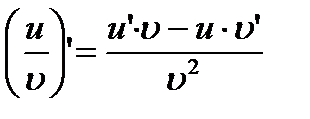
Пример:
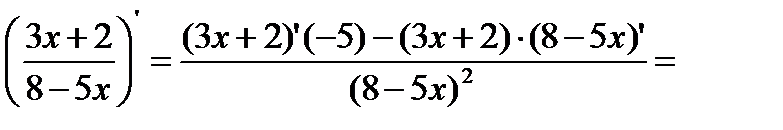
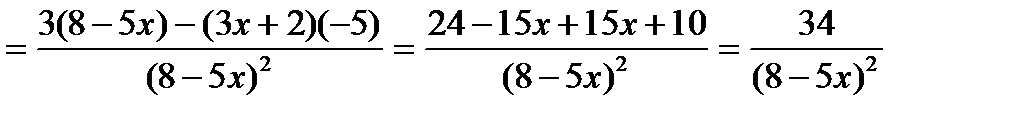
Производная сложной функции
Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) также имеет производную в точке x0, причем:
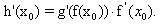
Найдем производную следующих функций:
1) 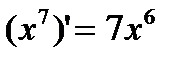
2) 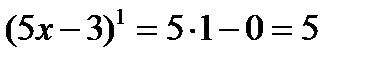
А теперь найдем производную сложной функции:
3) ((5х-3)7)’=7(5х-3)6 · (5х-3)1=7·5(5х-3)6= 35·(5х-3)6;
4) ((8+7х)-3)’= -3·(8+7х)-4 ·(8+7х)1= - 3·7(8+7х)-4 =
= - 21 ·(8+7х)-4
5) 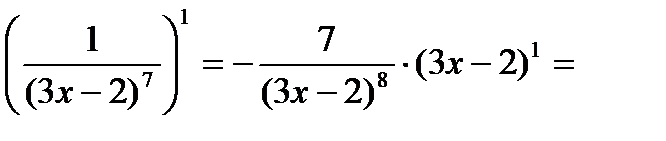
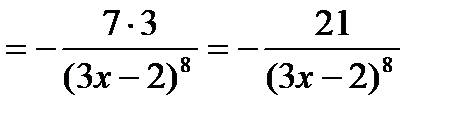
6) 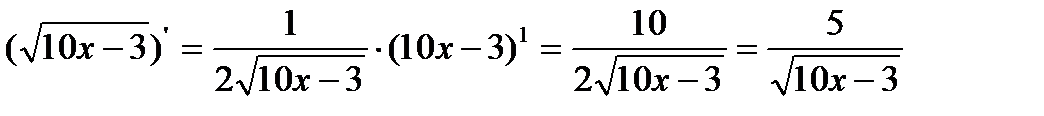
Контрольные вопросы
1. Дайте определения приращения аргумента и приращения функции, запишите соответствующие равенства и изобразите их на примере произвольной кривой линии.
2. Найдите приращение функции f в точке х0, если f(х) = 2х3 – 3, х0 = 3, Δх = - 0,2.
3. Дайте определение производной функции f в точке х0.
4. Найдите производную функции f(х) = кх + b (к и b – постоянные, т. е. числа) в точке х0.
5. Чему равна производная постоянной величины (константы)?
6. Каковы основные формулы дифференцирования (нахождения производных функций)?
7. Перечислите правила нахождения производных функций.
8. Найти производную функции:
а) 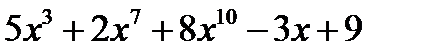
б) 4х·(3х+5)
в) 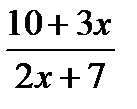
9. Запишите правило нахождения производной сложной функции.
10. Найдите производную функции:
1) (12х-7)10 2) 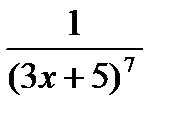
 2022-01-07
2022-01-07 165
165







