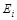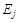Цепь – это такая последовательность ребер (дуг) графа, при которой для каждого ребра (дуги) (кроме первого и последнего) одна из его вершин является общей с предыдущим ребром (дугой), а вторая – с последующим.
Цель данной задачи состоит в определении кратчайшего маршрута от исходной вершины сети до завершающей.
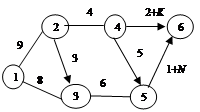
Задача 3.9. Фермер планирует доставлять часть сельскохозяйственной продукции фермерского хозяйства на переработку. Требуется проложить кратчайший маршрут от фермерского хозяйства до перерабатывающего цеха ассоциации фермерских хозяйств, используя существующую сеть дорог (рис. 3.10, а – в).
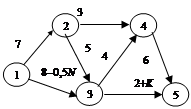 |
а
 |
б
 |
в
Рис. 3.10. Сеть дорог
На основании приведенной информации задачи 3.9, применив алгоритм Дейкстры, необходимо:
1) присвоить исходной вершине постоянную метку [0, –] и пометить в круглых скобках номер шага (1);
2) определить временные метки для всех вершин, которых можно достичь из выбранной вершины, согласно пункту 1 (при этом данные вершины не должны иметь постоянных меток) следующим образом:
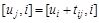 , при
, при 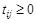 ,
,
где i – номер начальной вершины дуги (ребра) (i, j);
j – номер конечной вершины дуги (ребра) (i, j);
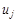 – расстояние к вершине j;
– расстояние к вершине j;
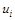 – кратчайшее расстояние к вершине i;
– кратчайшее расстояние к вершине i;
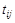 – длина дуги (ребра) (i, j);
– длина дуги (ребра) (i, j);
3) если вершина имеет две временные метки и более, то их заменить на постоянную метку, выбрав наименьшее расстояние между вершинами;
4) выбрав последнюю вершину с постоянной меткой, алгоритм продолжить выполнять с пункта 2 до тех пор, пока все вершины не будут иметь постоянных меток;
5) определить кратчайшую цепь, проходя этот путь в обратном направлении, используя постоянные метки;
6) рассчитать длину кратчайшего маршрута.
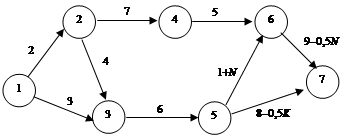
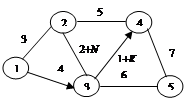
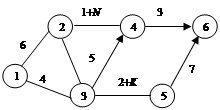
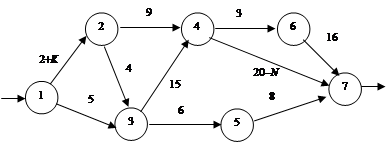
 Задача 3.10. Необходимо составить кратчайший маршрут от перерабатывающего предприятия до фирменного магазина, используя существующую сеть дорог (рис. 3.11, а – в).
Задача 3.10. Необходимо составить кратчайший маршрут от перерабатывающего предприятия до фирменного магазина, используя существующую сеть дорог (рис. 3.11, а – в).
 | |||
 | |||
а б
в
Рис. 3.11. Сеть дорог
На основании приведенной информации задачи 3.10, применив алгоритм Флойда, необходимо:
1) представить сеть в виде матрицы расстояний 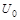 (табл. 3.4).
(табл. 3.4).
Т а б л и ц а 3.4. Матрица расстояний 
|
|
| ||||
| … | 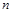
| ||||
| – | а12 | а13 | … | 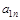
| |
| а21 | – | а23 | … | 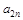
| |
| а31 | а32 | – | … | 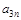
| |
| … | … | … | … | – | … |
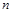
| 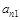
| 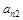
| 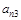
| … | – |
При определении элементов матрицы расстояний учитывать следующее: если вершина 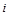 связана с вершиной
связана с вершиной 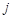 путем
путем 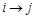 , то его расстояние
, то его расстояние 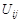 занести в таблицу, в противном случае такое расстояние принять равным бесконечности. Элементы матрицы
занести в таблицу, в противном случае такое расстояние принять равным бесконечности. Элементы матрицы 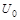 симметричны относительно главной диагонали, за исключением пар элементов, соединенных между собой дугами, а не ребрами;
симметричны относительно главной диагонали, за исключением пар элементов, соединенных между собой дугами, а не ребрами;
2) представить сеть в виде матрицы последовательности вершин 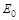 (табл. 3.5);
(табл. 3.5);
Т а б л и ц а 3.5. Матрица последовательности вершин 
|
|
| ||||
| … | 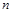
| ||||
| – | … | 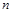
| |||
| – | … | 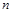
| |||
| – | … | 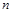
| |||
| … | … | … | … | – | … |
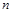
| … | – | |||
3) принять за ведущие первую строку и первый столбец (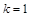 ) матрицы расстояний
) матрицы расстояний 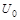 ;
;
4) рассмотреть возможность применения треугольного оператора ко всем элементам 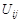 матрицы
матрицы 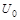 (рис. 3.12). Суть треугольного оператора Флойда: над элементами матрицы расстояний выполнить процедуру замены
(рис. 3.12). Суть треугольного оператора Флойда: над элементами матрицы расстояний выполнить процедуру замены
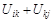 на
на 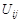 , если
, если 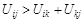 ;
;
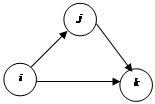 |
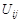
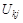
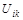
Рис. 3.12. Треугольный оператор Флойда
5) рассчитать новые элементы матрицы расстояний 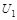 путем замены в матрице расстояний
путем замены в матрице расстояний 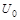 элемента
элемента 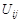 на сумму элементов
на сумму элементов 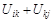 ;
;
6) определить новые элементы матрицы последовательности вершин 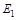 путем замены в матрице последовательности вершин
путем замены в матрице последовательности вершин 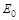 соответствующих элементов на элементы, равные номеру ведущей строки и столбца;
соответствующих элементов на элементы, равные номеру ведущей строки и столбца;
7) принять за ведущие вторую строку и второй столбец (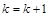 ) и алгоритм расчетов повторять с пункта 3 до тех пор, пока ни один элемент матрицы расстояний нельзя будет улучшить;
) и алгоритм расчетов повторять с пункта 3 до тех пор, пока ни один элемент матрицы расстояний нельзя будет улучшить;
8) используя конечную матрицу последовательности вершин 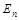 , найти кратчайший путь от исходной до завершающей вершины сети;
, найти кратчайший путь от исходной до завершающей вершины сети;
9) используя конечную матрицу расстояний 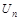 , найти длину кратчайшего пути от исходной до завершающей вершины сети.
, найти длину кратчайшего пути от исходной до завершающей вершины сети.
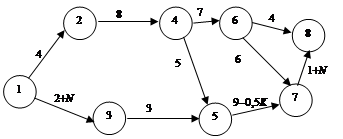
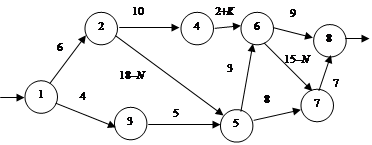
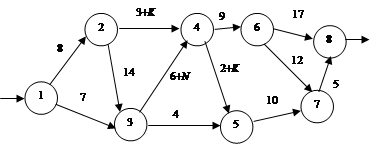
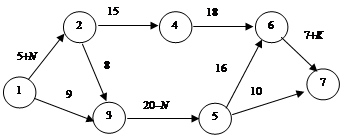
 Задача 3.11. Необходимо составить кратчайший маршрут от оптовой базы до магазина РайПО, используя существующие потоки сети (рис. 3.13, а – в).
Задача 3.11. Необходимо составить кратчайший маршрут от оптовой базы до магазина РайПО, используя существующие потоки сети (рис. 3.13, а – в).
а
 |
б
 |
в
Рис. 3.13. Входные и выходные потоки сети
На основании приведенной информации задачи 3.11, используя прямую задачу линейного программирования, необходимо:
1) сделать предложение о том, что в исходную вершину входит одна единица внешнего потока, которая и выходит из завершающей вершины сети;
2) ввести двоичные переменные задачи:
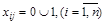 ,
,
где 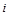 – номер вершины, из которой выходит поток;
– номер вершины, из которой выходит поток;
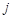 – номер вершины, в которую входит поток;
– номер вершины, в которую входит поток;
3) записать ограничения задачи в виде баланса потока, т. е. общий входной поток минус общий выходной поток, равный нулю;
4) составить целевую функцию задачи, позволяющую минимизировать длину сети:
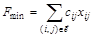 ,
,
где 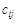 – расстояние от вершины сети
– расстояние от вершины сети 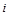 до вершины
до вершины 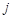 ;
;
5) решить прямую задачу линейного программирования с помощью электронных матриц Excel;
6) проанализировав оптимальное решение задачи, найти кратчайший путь из исходной вершины до завершающей вершины сети и определить его длину.
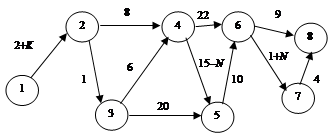
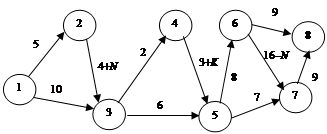
 Задача 3.12. Требуется обосновать кратчайший маршрут от центра кооперативного участка до базы райпотребсоюза, используя существующую сеть дорог (рис. 3.14, а – в).
Задача 3.12. Требуется обосновать кратчайший маршрут от центра кооперативного участка до базы райпотребсоюза, используя существующую сеть дорог (рис. 3.14, а – в).
 а
а
 б
б
в
Рис. 3.14. Сеть дорог для выбора кратчайшего пути
На основании приведенной информации задачи 3.12, используя двойственную задачу линейного программирования, необходимо:
1) ввести неизвестные величины задачи:
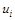 – расстояние от исходной вершины до вершины сети i;
– расстояние от исходной вершины до вершины сети i;
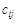 – длина дуги (ребра) (i, j);
– длина дуги (ребра) (i, j);
2) расстояние до исходной вершины сети принять равным нулю: 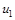 = 0;
= 0;
3) составить ограничения двойственной задачи:
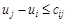 ,
,
где 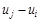 – расстояние от вершины i до вершины сети j;
– расстояние от вершины i до вершины сети j;
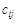 – длина дуги (ребра) (i, j);
– длина дуги (ребра) (i, j);
4) записать целевую функцию задачи, позволяющую максимизировать расстояние от исходной вершины сети 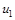 до завершающей
до завершающей 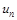 :
:
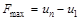 ;
;
5) решить двойственную задачу линейного программирования с помощью электронных таблиц Excel;
6) проанализировать оптимальное решение задачи и определить, используя значения двойственных переменных, равных единице, кратчайший путь из исходной вершины сети до завершающей;
7) вычислить длину кратчайшего пути.
 2022-01-07
2022-01-07 175
175