Поток – это экономическая величина, измеряемая в движении с учетом того периода времени, для которого делается расчет.
Задача 3.13. Требуется обосновать максимальную величину потока комбикормов, поступающих из комбикормового завода на птицефабрику, используя следующую сеть (рис. 3.15, а – в).
 |
а

б
 |
в
Рис. 3.15. Сеть для определения максимального потока
Используя информацию задачи 3.13, применив алгоритм Форда, необходимо:
1) сформировать матрицу пропускных способностей дуг (ребер) сети. При этом в метку (i, j) записывают пропускную способность дуги ( ), если она больше нуля; если пропускная способность симметричной ей дуги равна нулю, то в клетку (j, i) ставят нуль; если
), если она больше нуля; если пропускная способность симметричной ей дуги равна нулю, то в клетку (j, i) ставят нуль; если  , то клетки (i, j) и (j, i) не заполняют;
, то клетки (i, j) и (j, i) не заполняют;
2) пометить значком * столбец Е1 матрицы пропускных способностей;
3) найти в строке Е1 положительные элементы матрицы ( ) и столбцы, в которых они находятся, пометить номером просматриваемой строки;
) и столбцы, в которых они находятся, пометить номером просматриваемой строки;
4) продолжить процедуру пометок до тех пор, пока:
а) не будет помечен столбец 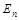 , т. е. сток;
, т. е. сток;
б) нельзя пометить новые столбцы, что означает отсутствие пути из Е1 в 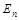 , проходящего по дугам с положительной пропускной способностью;
, проходящего по дугам с положительной пропускной способностью;
5) найти путь из стока Е1 в сток 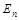 , используя пометки столбцов;
, используя пометки столбцов;
6) расставить знаки, используя соответствующие элементы сети  . Последний положительный элемент столбца
. Последний положительный элемент столбца 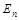 , т. е.
, т. е.  , пометить знаком «–», а симметричный ему элемент – знаком «+». Процесс пометок продолжить до тех пор, пока не придем к истоку (вершине Е1) и не отметим знаком «–» элемент этой строки и знаком «+» симметричный ему элемент;
, пометить знаком «–», а симметричный ему элемент – знаком «+». Процесс пометок продолжить до тех пор, пока не придем к истоку (вершине Е1) и не отметим знаком «–» элемент этой строки и знаком «+» симметричный ему элемент;
7) определить пропускную способность пути  , которая равна наименьшей из пропускных способностей дуг пути, получивших знак «–»:
, которая равна наименьшей из пропускных способностей дуг пути, получивших знак «–»:
 ;
;
8) определить остаточные пропускные способности дуг пути и симметричных к ним дуг, т. е. из элементов таблицы  , получивших знак «–», вычесть выбранный элемент
, получивших знак «–», вычесть выбранный элемент  , а к элементам
, а к элементам  , получивших знак «+», прибавить
, получивших знак «+», прибавить  ;
;
9) все изменения элементов  занести в новую матрицу пропускных способностей дуг (ребер) и расчеты повторять с пункта 2 до тех пор, пока не получим матрицу
занести в новую матрицу пропускных способностей дуг (ребер) и расчеты повторять с пункта 2 до тех пор, пока не получим матрицу  , в которой нет ни одного пути из истока Е1 в сток
, в которой нет ни одного пути из истока Е1 в сток 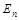 с пропускной способностью больше нуля;
с пропускной способностью больше нуля;
10) вычислить элементы новой таблицы путем вычитания из элементов матрицы последовательности дуг (ребер)  соответствующих элементов матрицы
соответствующих элементов матрицы  ;
;
11) используя положительные элементы таблицы, охарактеризовать величины дуговых потоков;
12) определить величину максимального потока сети, просуммировав элементы строки Е1 (источника) или элементы столбца 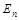 (стока);
(стока);
13) найти дуги, образующие разрез с минимальной пропускной способностью. При этом учесть, что данный разрез образован дугами, начальные вершины которых характеризуют строки Е1, а конечные вершины – элементы столбца 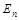 ;
;
14) сделать вывод о степени насыщения дуг разреза потоком.
Задача 3.14. Необходимо обосновать максимальную пропускную способность потока зерна, поступающего из сельскохозяйственного предприятия на элеватор, используя следующую сеть (рис. 3.16, а – в).
Используя информацию задачи 3.14, необходимо:
1) ввести неизвестные величины задачи линейного программирования 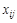 , обозначающие поток по дуге (ребру) (
, обозначающие поток по дуге (ребру) (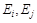 ), равный количеству вещества, перемещаемого по ней в единицу времени;
), равный количеству вещества, перемещаемого по ней в единицу времени;
2) составить развернутую задачу линейного программирования, используя следующую структурную экономико-математическую модель.
Требуется найти значения 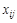 , максимизирующие одну из целевых функций:
, максимизирующие одну из целевых функций:
а) максимальный поток, равный количеству вещества, вытекающего из источника:
 ,
,
б) или максимальный поток, равный количеству вещества, притекающего в сток:
 .
.
При условиях:
1. По предельной пропускной способности дуг –
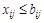 ,
, 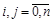 ,
, 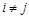 .
.
2. По балансу вещества, притекающего в любую промежуточную вершину и вытекающего из нее –
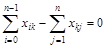 ,
, 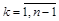 .
.
3. Неотрицательность переменных –
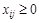 ;
;

а
 |
б
 |
в
Рис. 3.16. Сеть дорог для определения максимального потока
3) решить задачу, используя электронные таблицы Excel (Поиск решения);
4) проанализировать оптимальное решение экономико-математи-ческой задачи, определив величины дуговых потоков, разрезы с минимальной пропускной способностью и величину максимального потока сети.
 2022-01-07
2022-01-07 94
94








