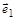2022-01-07
159
Граф – с одной стороны, это совокупность двух множеств: множества элементов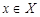 
и множества отношений между этими элементами; с другой стороны, это некая геометрическая схема, в которой элементы множества Х выступают точками или вершинами, а отношения между ними выражены отрезками (ребрами) или дугами (направленными ребрами), соединяющими элемент Х с элементами, которые с ним связаны.
В экономике широкое использование получил такой граф, как сеть.
Сеть – это ориентированный конечный связный граф без контуров, имеющий начальную (источник) и конечную (сток) точки.
Задача 3.1. Требуется построить сетевой график, заданный перечнем работ (табл. 3.1).
Т а б л и ц а 3.1. Перечень работ
| Работа (i, j) | Продолжительность, дн. |
| 1, 2 | |
| 1, 3 | |
| 2, 3 | |
| 2, 4 | |
| 2, 5 | |
| 3, 4 | |
| 4, 5 | |
| 4, 6 | |
| 5, 6 |
Задача 3.2. Требуется построить сетевой график, заданный структурной таблицей (табл. 3.2).
Т а б л и ц а 3.2. Структурная таблица
| Дуга орграфа | Опирается на дуги |
| – |
| – |
| – |
|
|
|
|
| ,
|
|
|
| ,
|
| ,
|
| ,
|
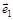
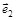
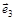
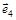
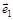
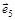
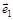
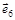
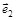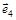
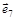
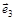
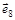
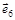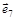
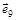
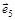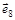
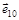
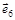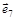
Задача 3.3. Построить матрицу инциденций для ребер неориентированного графа и дуг орграфа, представленных на рис. 3.1 и 3.2.
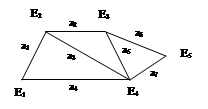
Рис. 3.1. Неориентированный Рис. 3.2. Орграф
граф
При этом матрицей инциденций для дуг орграфа является матрица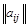 
,строки (m) которой соответствуют вершинам, столбцы (n) – дугам, а каждый элемент 
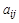формируется следующим образом:
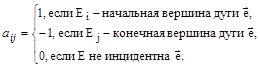
Если имеем неориентированный граф, то элементы матрицы 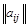размером m× n формируются таким образом:
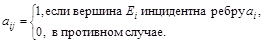
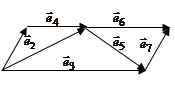
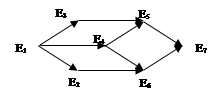
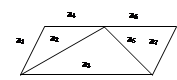Задача 3.4. Построить матрицу смежности ребер и дуг неориентированного графа и орграфа, представленных на рис. 3.3 и 3.4.
|
Рис. 3.3. Неориентированный Рис. 3.4. Орграф
граф
При этом матрицей смежности дуг (ребер) орграфа (неориентированного графа) называется матрица А, каждый элемент которой 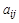равен 1, если конечная вершина дуги 
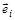является начальной вершиной дуги 
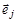(если ребра имеют общую вершину), и нулю в остальных случаях:
а)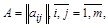 
где m – число ребер неориентированного графа,
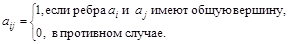
б)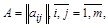
где m – число дуг орграфа,
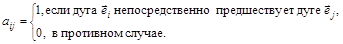
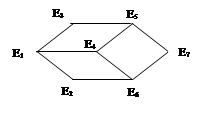Задача 3.5. Построить матрицу смежности вершин для неориентированного графа (рис. 3.5) и орграфа (рис. 3.6).
Рис. 3.5. Неориентированный Рис. 3.6. Орграф
граф
При этом матрицей смежности вершин орграфа является квадратная матрица А, каждый элемент которой 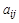численно равен количеству дуг, идущих из вершины 
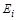в вершину 
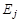. Следует отметить, что матрица смежности вершин орграфа является не симметричной относительно главной диагонали. Для неориентированного графа матрица смежности вершин является симметричной, так как ребра 
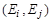и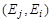 
существуют одновременно.
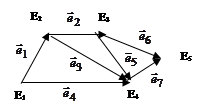
Задача 3.6. Требуется разбить элементы орграфа по рангам (слоям) и упорядочить их для орграфа, изображенного на рис. 3.7.
 |
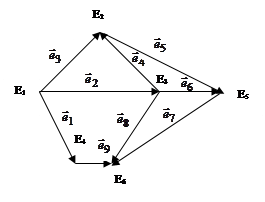Рис. 3.7. Неупорядоченный орграф
Используя приведенную информацию, упорядочить орграф с помощью графического способа:
1) суть графического способа упорядочения элементов орграфа состоит в последовательном нахождении вершины, степень входящих дуг которой равна нулю: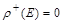 
. Такая вершина Еi является вершиной 1-го ранга. Вершина называется вершиной 2-го ранга, если в нее входят несколько дуг из вершин 1-го ранга, и не входит ни одна дуга из вершин выше 1-го ранга. Вершина Еi называется вершиной k -го ранга, если в нее входят дуги из вершин не выше (k–1)-го ранга, и при этом имеется хотя бы одна дуга, исходящая из вершин (k–1)-го ранга. Дуга 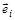называется дугой k-го ранга, если она опирается на дугу (дуги) не выше (k–1)-го ранга, среди которых есть хотя бы одна дуга (k–1)-го ранга;
2) после разбиения на ранги элементам орграфа придать более удобную нумерацию, такую, чтобы:
а) все номера элементов некоторого ранга были меньше номеров элементов следующего ранга; номера элементов 1-го ранга были наименьшими, а номера элементов последнего ранга – наибольшими;
б) порядок элементов внутри одного и того же ранга был безразличен (так как вершины, принадлежащие одному рангу, не соединены между собой дугами, а дуги друг на друга не опираются).
Таким образом, графический способ упорядочения вершин (алгоритм Фалкерсона) состоит из следующих шагов:
а) находят вершины первого ранга и пронумеровывают их (1, 2…);
б) мысленно вычеркивают все пронумерованные вершины (1-го ранга) и дуги из них выходящие;
в) вершины, оставшиеся без входящих дуг, относят ко второму рангу и присваивают им очередные номера и т. д.;
г) шаги п. б) и в) повторяют до тех пор, пока все вершины не будут пронумерованы;
3) изобразить упорядоченный орграф по рангам вершин;
4) аналогично, используя графический способ, определить ранги дуг. Найти дуги, не имеющие непосредственно предшествующих дуг. Они образуют 1-й ранг. После их мысленного вычеркивания вновь найти дуги, не имеющие непосредственно предшествующих (это дуги 2-го ранга). И так до тех пор, пока все дуги не будут разбиты на ранги.
При этом дуги, выходящие из вершин конкретного ранга, относятся к этому же рангу;
5) изобразить упорядоченный по рангам дуг орграф.
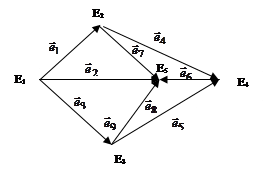Задача 3.7. Требуется упорядочить орграф, используя матрицу смежности вершин орграфа (рис. 3.8).
Рис. 3.8. Неупорядоченный орграф
Используя приведенную информацию, упорядочить орграф с помощью метода Демукрона, основанного на использовании матрицы смежности вершин орграфа:
1) обозначить через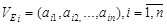 
векторы, являющиеся строками матрицы смежности;
2) вычислить компоненты вектора V1:
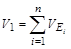
и поместить результат в (n+1)-ю строку табл. 3.3;
Т а б л и ц а 3.3. Матрица смежности вершин
| Номер строки | Ei | Еj | Ранг | Новая нумерация вершин | ||||||
| Е1 | … | Ek | … | Es | … | En | ||||
| E1 | a11 | … | a1k | … | a1s | … | a1n | r |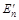 
| |
| … | … | … | … | … | … | … | … | … | … | … |
| k | Ek | ak1 | … | akk | … | aks | … | akn |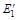 
| |
| … | … | … | … | … | … | … | … | … | … | … |
| s | Es | as1 | … | ask | … | ass | … | asn |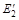 
| |
| … | … | … | … | … | … | … | … | … | … | … |
| n | En | an1 | … | ank | … | ans | … | ann |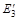 
| |
| n+1 | V1 |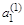 
| … | 
| … | 
| … | 
|
| |
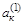
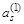
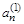
| n+2 | V2 |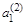 
| … | 
| … | 
| … | 
| ||
| … | … | … | … | … | … | … | … | … | ||
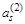
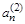
| n+r | Vr | … | … | … | ||||||
3) среди неотрицательных компонентов вектора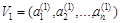 
найти компоненты, равные нулю.
Пусть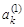 
и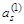 
равны нулю. Это значит, что в вершины Ек и Es не входит ни одна дуга, и они относятся к 1-му рангу. В столбце, соответствующем рангу, в строках k и s записать ранг этих вершин;
4) из вектора V1 вычесть векторы-строки, соответствующие вершинам 1-го ранга Ек и Es;
5) в результате вычисления получен вектор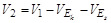 
, в котором появятся новые компоненты, равные нулю. Пусть 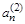=0. Следовательно, вершина En относится ко 2-му рангу. Ранг этой вершины, равный 2, занести в таблицу;
6) вычислить вектор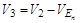 
, в котором появятся новые нули. Следовательно, определить вершины 3-го ранга;
7) аналогичным образом продолжить процесс вычисления до тех пор, пока не будет получен вектор, все компоненты которого равны нулю. Пусть Vr – нулевой вектор, новый нулевой компонент которого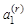 
. Тогда Е1 – вершина r -го ранга;
8) перенумеровать вершины орграфа согласно их рангам и записать новые номера в последний столбец табл. 3.3;
9) построить упорядоченный орграф.
