2022-01-07
238
Задача нахождения потока минимальной стоимости в сети с ограниченной пропускной способностью обобщает задачу определения максимального потока, так как каждой дуге (ребру) соответствует определенная стоимость прохождения единицы потока по этой дуге (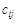
).
Задача 3.15. Требуется минимизировать стоимость в сети с ограниченной пропускной способностью В =15. Сеть (рис. 3.17, а – в) дополнена стоимостью прохождения единицы потока по дугам (ребрам) 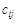, информация о которой записана в скобках над дугами (ребрами) сети.
Используя информацию задачи 3.15, необходимо:
1) ввести переменные величины задачи линейного программирования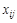 
, обозначающие величину потока по дуге (ребру) (
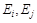), перемещаемого по ней в единицу времени;
2) составить развернутую задачу, используя следующую структурную экономико-математическую модель.
Требуется минимизировать стоимость потока в сети:
.
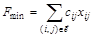При условиях:
1. По предельной пропускной способности дуг –
, 
, 
.
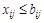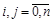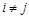2. По балансу вещества, притекающего в любую промежуточную вершину и вытекающего из нее –
, 
.
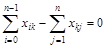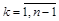3. По количеству вещества, вытекающего из источника и притекающего в сток –
а)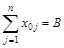 
;
б)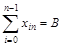 
.
4. Неотрицательность переменных –
;
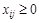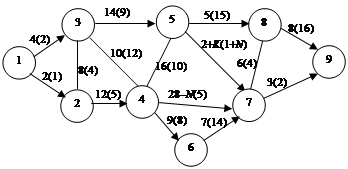
а
 |
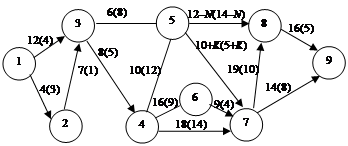б
 |
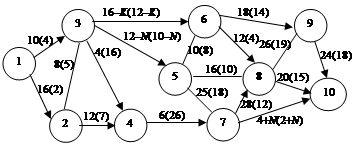в
Рис. 3.17. Сеть для определения потока минимальной стоимости
3) решить задачу линейного программирования, используя электронные таблицы Excel;
4) сделать анализ оптимального решения экономико-математи-ческой задачи, определив разрезы с минимальной пропускной способностью, величины дуговых потоков, величину потока сети и его минимальную стоимость в сети.
