2. Векторная алгебра и анализ
2.2. Векторная алгебра, аналитическая геометрия
Автор Л.Ю. Трояновская.
Содержание:
- Поверхность в пространстве. ♦
- Уравнение плоскости в пространстве. ♦
- Уравнение линии в пространстве. ♦
- Уравнение прямой линии в пространстве. ♦
- Плоскость и прямая в пространстве. ♦
Поверхность в пространстве.
Определение 1.Уравнением данной поверхности в декартовой системе координат называется такое уравнение 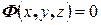 , что ему удовлетворяют координаты всех точек, лежащих на этой поверхности и не удовлетворяют координаты точек не лежащих на этой поверхности.
, что ему удовлетворяют координаты всех точек, лежащих на этой поверхности и не удовлетворяют координаты точек не лежащих на этой поверхности.
С помощью уравнения поверхности можно исследовать ее форму и ориентацию в пространстве не геометрически, а аналитически. Уравнение поверхности отражает некоторое, общее для всех точек данной поверхности, свойство.
Самая простая поверхность – это плоскость.
Уравнение плоскости в пространстве.
Чтобы составить уравнение плоскости, отражающее некоторое общее свойство точек данной плоскости, нужно это свойство сформулировать.
Уравнение плоскости, проходящей через три заданные точки.
Задача 1.Составить уравнение плоскости, проходящей через точки 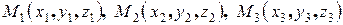 .
.
Решение.
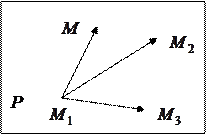 Возьмем произвольную точку
Возьмем произвольную точку 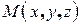 и потребуем, чтобы она тоже лежала на данной плоскости. Для этого построим три вектора, исходящие из одной точки:
и потребуем, чтобы она тоже лежала на данной плоскости. Для этого построим три вектора, исходящие из одной точки:
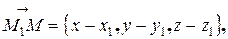
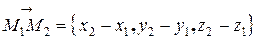 ,
,
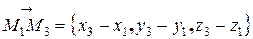 .
.
Тогда, чтобы все три вектора (а, значит, и все четыре точки) лежали в одной плоскости, должно выполняться условие компланарности трех векторов:
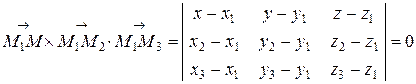 .
.
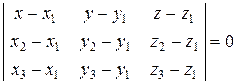 Т.о., все точки, координаты которых удовлетворяют этому уравнению, лежат на той же плоскости, что и точки
Т.о., все точки, координаты которых удовлетворяют этому уравнению, лежат на той же плоскости, что и точки 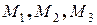 . Следовательно,
. Следовательно,
− уравнение плоскости, проходящей через три заданные точки.
Пример.
Составить уравнение плоскости Р, проходящей через точки 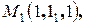
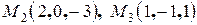 .
.
Решение.
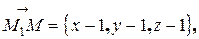
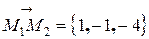 ,
,
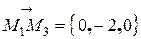 .
.
Уравнение запишется так:
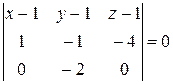 − разложим определитель по первой строке:
− разложим определитель по первой строке:
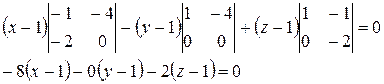
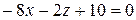 − умножим обе части уравнения на (-1), получим
− умножим обе части уравнения на (-1), получим 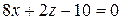
Ответ: Р: 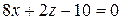 .
.
Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.
Задача 2.Составить уравнение плоскости Р, проходящей через точку 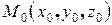 перпендикулярно вектору
перпендикулярно вектору 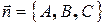 .
.
Решение.
Возьмем точку М с произвольными координатами (х, у, z) и потребуем, чтобы эта точка лежала на той же плоскости, что и точка 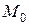 . Для этого построим вектор.
. Для этого построим вектор. 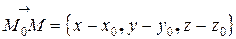 Т.к. вектор
Т.к. вектор  перпендикулярен плоскости, то он перпендикулярен любому вектору, лежащему в этой плоскости.
перпендикулярен плоскости, то он перпендикулярен любому вектору, лежащему в этой плоскости.
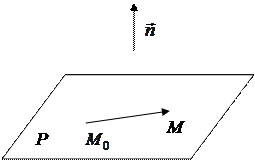 Запишем условие ортогональности двух векторов:
Запишем условие ортогональности двух векторов:
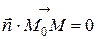
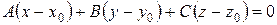 − это и есть уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.
− это и есть уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.
Раскроем скобки и приведем подобные:
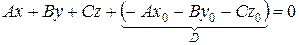
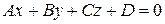 − общее уравнение плоскости.
− общее уравнение плоскости.
Здесь А, В, С – координаты вектора, перпендикулярного плоскости.
Определение 2.Любой вектор, перпендикулярный плоскости, называется ее нормальным вектором (или ее вектором нормали). Обозначение: 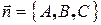 .
.
Все векторы нормали к одной плоскости коллинеарны.
Пример.
Составить уравнение плоскости Р, проходящей через точку 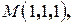 перпендикулярно вектору
перпендикулярно вектору 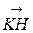 , если К( 0, 2, 1), Н( 2, 3, 7).
, если К( 0, 2, 1), Н( 2, 3, 7).
Решение.
Воспользуемся уравнением 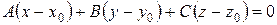 . Здесь А, В, С – координаты вектора
. Здесь А, В, С – координаты вектора 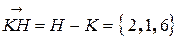 , а
, а 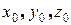 − координаты точки М. Получим
− координаты точки М. Получим 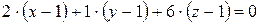
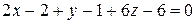 . Приводя подобные, получим
. Приводя подобные, получим
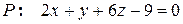 .
.
Ответ: 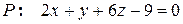 .
.
Нормальное уравнение плоскости.
Задача 3.Составить уравнение плоскости Р, проходящей на расстоянии ρ от начала координат в направлении перпендикуляра, опущенного из начала координат на плоскость и имеющего с координатными осями 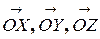 углы α, β, γ соответственно.
углы α, β, γ соответственно.
Решение.
 Единичный вектор перпендикуляра, опущенного из начала координат на плоскость Р − это вектор
Единичный вектор перпендикуляра, опущенного из начала координат на плоскость Р − это вектор 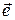 . Его координаты – направляющие косинусы этого перпендикуляра, т.е.,
. Его координаты – направляющие косинусы этого перпендикуляра, т.е., 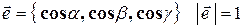 . Выберем на плоскости произвольную точку
. Выберем на плоскости произвольную точку 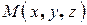 . Вектор, соединяющий начало координат с этой точкой называется ее радиус-вектором и имеет те же координаты
. Вектор, соединяющий начало координат с этой точкой называется ее радиус-вектором и имеет те же координаты 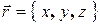 . Не зависимо от положения точки М на плоскости, проекция ее радиус-вектора на вектор
. Не зависимо от положения точки М на плоскости, проекция ее радиус-вектора на вектор 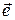 всегда равна ρ. Имеем:
всегда равна ρ. Имеем: 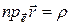 , но
, но 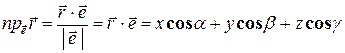 , следовательно,
, следовательно, 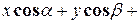
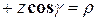 . Окончательно:
. Окончательно:
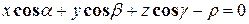 − нормальное уравнение плоскости.
− нормальное уравнение плоскости.
Общее уравнение плоскости 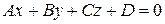 можно привести к нормальному виду, умножив обе части равенства на нормирующий множитель
можно привести к нормальному виду, умножив обе части равенства на нормирующий множитель 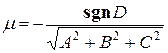 . Здесь
. Здесь 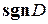 − это функция, значение которой равно -1, если D ‹ 0, и равно 1, если D › 0. Другими словами, знак нормирующего множителя противоположен знаку свободного члена общего уравнения.
− это функция, значение которой равно -1, если D ‹ 0, и равно 1, если D › 0. Другими словами, знак нормирующего множителя противоположен знаку свободного члена общего уравнения.
Пример.
Записать уравнение плоскости 2x + y −z+5=0 в нормальном виде.
Решение.
Нормирующий множитель равен
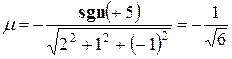
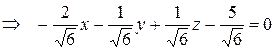 − это ответ.
− это ответ.
Уравнение плоскости в отрезках, отсекаемых на координатных осях.
Задача 4. Изобразить на чертеже плоскость, отсекающую на осях координат 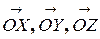 отрезки а, b и с соответственно.
отрезки а, b и с соответственно.
Решение.
Плоскость − объект бесконечный и изобразить ее всю невозможно, но можно построить линии пересечения с координатными плоскостями, т.к. известны точки пересечении данной плоскости с координатными осями − это 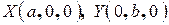 и
и 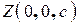 . Подставим координаты этих точек в уравнение плоскости, проходящей через три заданные точки. Получим
. Подставим координаты этих точек в уравнение плоскости, проходящей через три заданные точки. Получим 
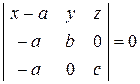 .
.
Вычислив определитель, получим 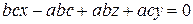 . Перенесем
. Перенесем 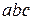 в правую часть и разделим на
в правую часть и разделим на 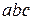 обе части равенства, получим
обе части равенства, получим 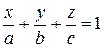 − уравнение плоскости в отрезках.
− уравнение плоскости в отрезках.
Пример.
Изобразить на чертеже плоскость 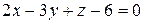 .
.
Решение.
Перейдем к уравнению в отрезках:

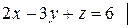 разделим обе части на 6
разделим обе части на 6
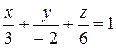 , следовательно, плоскость пересекает координатные оси в точках
, следовательно, плоскость пересекает координатные оси в точках 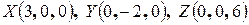 .
.
Ответ:
Взаимное расположение плоскостей в пространстве.
Взаимное расположение плоскостей в пространстве характеризуется взаимным расположением их нормальных векторов. Пусть заданы две плоскости 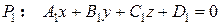 и
и 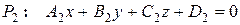 . Их векторы нормали, соответственно,
. Их векторы нормали, соответственно, 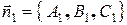 и
и 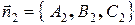 .
.
Тогда:
1. Углом между плоскостями считается меньший из двугранных углов, косинус которого равен: 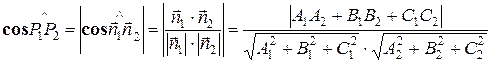 .
.
2. Условие параллельности двух плоскостей: 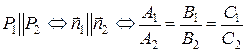 .
.
3. Условие перпендикулярности двух плоскостей: 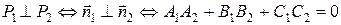 .
.
Пример.
Найти угол между плоскостями 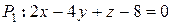 и
и 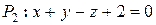 .
.
Решение.
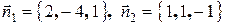 , следовательно,
, следовательно,
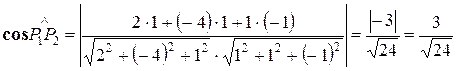 .
.
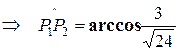 .
.
Ответ: 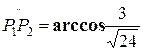 .
.
 2023-09-15
2023-09-15 1227
1227