2014-02-24
524
Опр.1. Проективное пространство, в котором какая-нибудь одна гиперплоскость выделена из остальных и названа «несобственной» или «бесконечно удаленной», называется проективно-аффинным пространством.
Рассмотрим, каким образом можно выделить в n-мерном проективном пространстве RPn его «несобственные» элементы точки, прямые, двумерные плоскости и т.д.
Пусть в n+1-мерном аффинном пространстве Аn+1 дано n-мерное подпространство Аn и в нём - аффинная система координат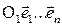 
. Назовём аффинную систему координат 
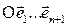пространства Аn+1 естественно связанной с координатной системой 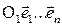n-мерного пространства Аn, если начало О системы координат 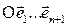не лежит в пространстве Аn. Первые n координатных векторов у этих координатных систем общие: 
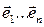, а последний вектор 
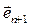есть вектор 
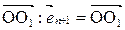. Тогда в системе координат 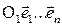подпространство Аn пространства Аn+1 задаётся уравнением: 
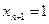. Возьмём теперь в пространстве An+1 связку с центром О. Если произвольная точка М гиперплоскости Аn имеет в системе 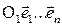координаты 
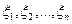, то координаты этой точки М в системе 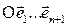следующие: 
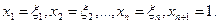Поэтому наборами координат луча 
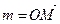связки О являются все наборы х1,х2,...,хn+1, пропорциональные набору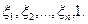 
Опр. 2. Все такие указанные наборы называются наборами однородных координат точки М в системе однородных координат, соответствующей аффинной координатной системе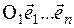 
.
Итак, однородные координаты х1,х2,...,хn+1 точки М связаны с её аффинными координатами 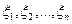в системе 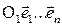пропорцией: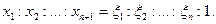 
Отсюда аффинные координаты выражаются через однородные по формулам: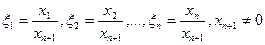 
.
Опр. 3. Соответствие между точками М гиперплоскости Аn и лучами 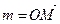связки О называется перспективным соответствием.
При этом каждой точке М гиперплоскости Аn, имеющей однородные координаты х1,х2,...,хn+1 соответствует луч связки О с такими же координатами в системе .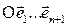
Обратно, каждому лучу m(х1,х2,...,хn+1) связки О, у которого последняя координата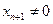 
, соответствует точка М гиперплоскости Аn с теми же координатами х1,х2,...,хn+1. Однако, лучам m связки О, у которых 
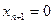, не соответствует никакая точка М гиперплоскости А n. Чтобы сделать перспективное соответствие между связкой О и гиперплоскостью Аn взаимно однозначным или биективным, дополним эту гиперплоскость несобственными или бесконечно удалёнными точками с наборами однородных координат х1,х2,...,хn,0. Пополненная таким образом гиперплоскость превращается в проективное пространство RPn = 
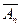. Это пространство становится арифметическим, если отождествить каждую его точку М с классом наборов ее однородных координат.
Замечание. Арифметическое проективное пространство естественно рассматривать как проективное пространство, полученное от пополнения несобственными элементами обыкновенного n-мерного аффинного пространства Аn с заданной в нём системой аффинных координат 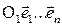. Несобственные точки этого пространства - это точки (х1,х2,...,хn+1), для которых 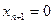, причем все такие точки принадлежат несобственной гиперплоскости с уравнением: 
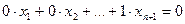или 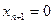. Преимущество однородной системы координат состоит в том, что несобственные точки получают вполне определенные координаты.
