2023-09-15
1444
Уравнение линии в пространстве.
Определение 3. Линией в пространстве называется линия пересечения двух поверхностей, а уравнением линии называется такая система уравнений
,
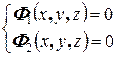что ей удовлетворяют координаты всех точек, лежащих на этой линии и не удовлетворяют координаты точек не лежащих на этой линии (т.е., координаты точек, одновременно принадлежащих обеим поверхностям).
При пересечении двух плоскостей в пространстве получается прямая линия.
Уравнение прямой линии в пространстве.
Пря мая линия бесконечна, поэтому для анализа ее положения в пространстве вводится понятие направляющего вектора.
Определение 4. Направляющим вектором прямой называется любой вектор, лежащий на этой прямой или параллельный ей. Обозначение: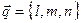 
.
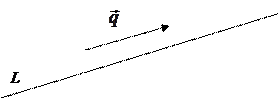
Общие уравнения прямой.
Задача 1. Найти линию пересечения двух плоскостей.
Решение.
Если линия образована пересечением двух плоскосте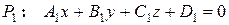й 
и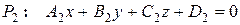 
, то система 
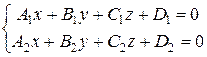− это общие уравнения прямой.
За направляющий вектор этой прямой можно принять векторное произведение нормальных векторов пересекающихся плоскостей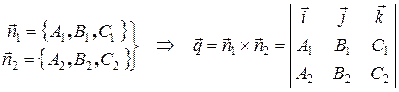 
.
Чтобы найти координаты точки, принадлежащей данной прямой, одну из координат задаем произвольно, например, z=0, а остальные находим из общих уравнений.
Пример.
Найти направляющий вектор и произвольную точку прямой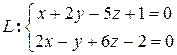 
.
Решение.
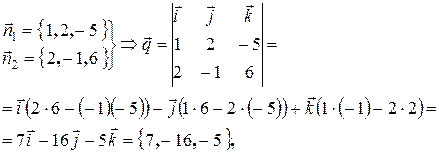
Пусть z =0. Потребуем, чтобы точка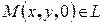 
. Подставим координаты точки в общие уравнения. Получим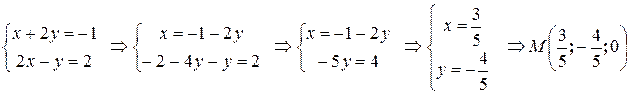 
Ответ: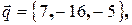 
.
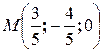Канонические уравнения прямой.
Задача 2. Составить уравнение прямой L, проходящей через точку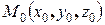 
параллельно вектору 
.
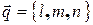Решение.
На прямой выберем произвольную точку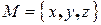 
и построим вектор 
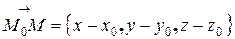. Запишем условие коллинеарности векторов 
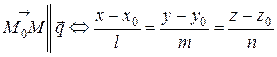− это канонические уравнения прямой.
Пример.
Написать канонические уравнения прямой, проходящей через точку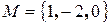 
параллельно вектору 
.
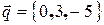Решение.
.
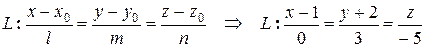Параметрические уравнения прямой.
Задача 3. Записать параметрические уравнения прямой, проходящей через точку 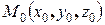параллельно вектору .
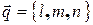Решение.
Запишем канонические уравнения этой прямой:
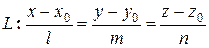т.к. все дроби равны, их можно обозначить одной буквой: 
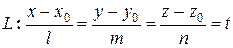. Тогда получим:
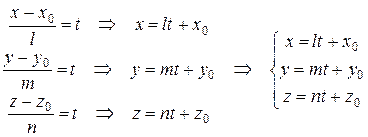− параметрические уравнения прямой.
Уравнение линии, проходящей через две заданные точки.
Задача 4. Найти прямую, проходящую через две заданные точк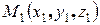и 
и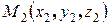 
.
Решение.
Воспользуемся каноническими уравнениями. За направляющий вектор можно принять вектор, лежащий на прямой – вектор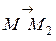 
, аза точку 
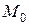принять, например, точку 
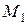. Получим:
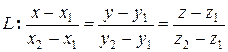− уравнение линии, проходящей через две заданные точки.
Взаимное расположение прямых в пространстве.
Взаимное расположение прямых в пространстве характеризуется взаимным расположением их направляющих векторов. Пусть заданы две лини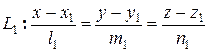и: 
и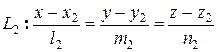 
. Тогда:
1. Угол между линиями – это меньший из вертикальных углов, поэтому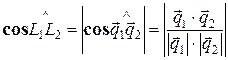 
.
2. Условие параллельности двух прямых
.
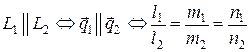3. Условие перпендикулярности двух прямых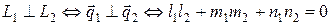 
.
Плоскость и прямая в пространстве.
Взаимное расположение прямой линии и плоскости в пространстве определяется взаимным расположением их направляющего и нормального векторов.
