35Доверительный интервал. Построение доп интервала для мат ожидания.
1  с доверит вер = 1-α, если
с доверит вер = 1-α, если
P(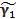 <
<  <
<  )≥1-α
)≥1-α
Для мат ожидания в лемме Фишера  *
* 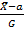 ∈N(0,1) оцениваем неизвa, G^2 знаем, находим число Z1-α/2 , такое что Ф(Z1-α/2)=1-α/2
∈N(0,1) оцениваем неизвa, G^2 знаем, находим число Z1-α/2 , такое что Ф(Z1-α/2)=1-α/2
P(-Z1-α/2 <  *
* 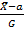 <Z1-α/2)= 1- α
<Z1-α/2)= 1- α
P(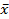 -
- 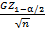 < a <
< a < 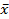 +
+ 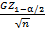 ) = 1- α
) = 1- α
(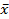 -
- 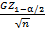 ;
; 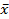 +
+ 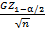 )
)
37Задачи проверки статистических гипотез, пример задач. Постановка задач, ошибки 1 и 2 ряда.
Пример: кубик 300 раз  P1=P2=P3=P4=P5=P6=1/6
P1=P2=P3=P4=P5=P6=1/6
X1,X2…Xn ~ F(x) F0(x)-извест ф-я распред
Гипотеза 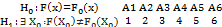 Если
Если  верно
верно 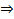 Pi=1/6
Pi=1/6
nPi = 50(300/6)  ^2=
^2=  =10,08 α=0,1; Z0,9=9,23
=10,08 α=0,1; Z0,9=9,23
В качестве 1ой гипотезы взять такую, чтобы ошиб 1 рода была min
Выработка критерия:
Возьмем α, 0< α<1 и ближе к 0, α  0
0
P(ошибка 1 рода)  α
α
P(ош 2 рода)→ min
38Критерий Колмогорова и хи-квадрат для проверки гипотезы согласия.
1)Колмогоров
Fn(t) – выбороч ф-я распред, Fn(t) = 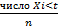
Dn=maxt∈R| 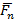 (t)-
(t)- 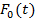 |
|
Теорема Колмогорова
H0 верна 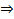 (
(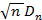 <x) n→беск → K(x) – функция распред Колмогорова
<x) n→беск → K(x) – функция распред Колмогорова
По таблk(x) ищем Z1-α:k(Z1- α ) = 1-α
Сравниваем  Z1- α
Z1- α 
2) Хи-квадрат 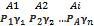 веществ прямую разбить на 2 зоны
веществ прямую разбить на 2 зоны
Pi=P(Xi∈Ai)  - число Xi попавших в зону Ai
- число Xi попавших в зону Ai
. 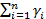 =nPi
=nPi 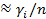 по ЗБЧ
по ЗБЧ  npi
npi
 ^2=
^2= 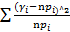
Теор Пирсона H0верна 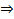 P(
P( ^2<x) →
^2<x) → 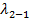 (x) – функция распредзак
(x) – функция распредзак  ^2(хи^2) с α задана по таблице
^2(хи^2) с α задана по таблице 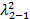 находим Z1-α : K2-1 (Z1-α)=1-α
находим Z1-α : K2-1 (Z1-α)=1-α
Сравниваем: 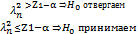
 2021-10-20
2021-10-20 61
61







