8)Независимые события. Виды независ Бернштейна
(Ω,F,P), A,B€F, P(A|B)=P(A)
Опр: A,B- независ↔P(A∩B)=P(A)*P(B)
Для большего числа соб:
A1,A2…An€F
1случай (попарная независимость)
Попарно незав, если ∀i=jAi,Aj-незав
2случай (взаимная независимость) вз. Нез,если∀k≤n и ∀ 1≤i1<i2…<ik≤n
P(Ai1∩Ai2∩..Ain)=к,j=1ПP(Aij)
Бернштейн. Подбросим тетраэдер. Цвета граней: К,Б,С+КБС
Ak=(внизу красный) Ас=(вн. Синий) Аб=(вн белый)
P(Ak)=1/2=P(Аб)=Р(Ас)
Р(Аб∩Ас)=1/2*1/2=1/4=Р(Аб)*Р(Ас)
Р(Ак∩Аб∩Ас)=1/4≠1/2*1/2*1/2≠Р(Ак)*Р(Аб)*Р(Ас)
Из взаимной следует попарная, но не наоборот
9) Испытания Бернулли. Фор-ла
n независимых испытаний Бернулли-это n испытаний с 2-мя исходами в каждом испытаний (называемыми условно «успехом» и «неудачей») И с постоянной вер успеха в каждом испытании
Н1Y2…Yn
P (при к-м испытании Y)=p ∀1≤k≤n
A=(в n испытаниях произошло =k успехов)
P(A)=?
Расм след цепочку из n эл-ов
(H1,H2,Y3…Hn-1,Yn)=P(H1)*P(H2)…P(Hn-1)*P(Yn)=p^k(1-p)^n-k
P(A)=Cn^k*p^k(1-p)^n-k=Pn(k) вер в nиспполучk успехов
Pn(n)=p^n
Pn(0)=(1-p)^n
Pn(≥1)=1-(1-p))^n
10)Лок пред теор Муавра-Лапласа
Xn,k=(k-np)/√npq, где q=1-p
∀k, таких, что |Xn,k|≤n^1/6-Ԑ
Pn(k)=(1/ /√npq)ϕ(Xn,k)
11. Интегральная предельная теорема Муавра-Лапласа. Формулировка и примеры.
Формулировка: Pn(a≤k≤b) ≈ 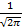 *
* 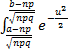 du
du
Доказательство:
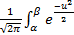 du =
du = 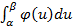
S= 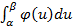 = Ф(𝞫)-Ф(𝞪)
= Ф(𝞫)-Ф(𝞪)
Ф(у)=  du
du
= Ф( )-Ф(
)-Ф(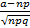 )
)
Пример:
1600 студентов. Р(число дней рождения летом 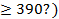
р=1/4.
Р1600 (390  ) = 1-Ф(-
) = 1-Ф(- 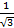 ) = 1-1+Ф(
) = 1-1+Ф( ) = Ф(
) = Ф( ).
).
12. Закон больших чисел в схеме Бернулли.
∀ε>0
Pn (| 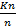 - p|≥ ε)
- p|≥ ε) 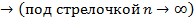 0, где Kn- число успехов в n испытаниях.
0, где Kn- число успехов в n испытаниях.
Pn (| 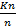 - p|
- p| 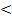 ε)
ε) 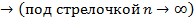 1
1
*p=P(Y). 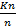 - частота успехов.
- частота успехов.
Доказательство:
Pn (| 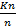 - p|≥ ε) = 1- Pn (|
- p|≥ ε) = 1- Pn (| 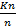 - p|
- p| 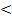 ε) =
ε) =  du – P(p-
du – P(p- 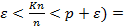 =
=  du – P(np-n
du – P(np-n 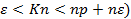 =
= 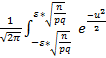 du+
du+ 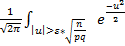 du – Pn(np-
du – Pn(np- 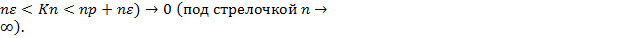
13. Теорема Пуассона в схеме серий испытаний Бернулли.
1я серия из 1 испытания с вероятностью успеха р1
2я серия из 2 испытаний ….. ……………....р2
n-я серия из n испытаний с вер успеха pn.
Пусть n*pn = λ 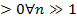 .
.
Тогда Pn (k) 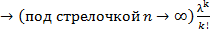 *e^(-λ) для любого фиксир к.
*e^(-λ) для любого фиксир к.
Если к-мало, то Pn(k) 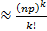 * e^(-np) p-малое, k-малое.
* e^(-np) p-малое, k-малое.
Доказательство:
К- фиксированное число.
Pn(k)=  * pn^k (1-Pn)^(n-k) =
* pn^k (1-Pn)^(n-k) =  *
*  * pn^k*(1-pn)^(n-k)*n^k=
* pn^k*(1-pn)^(n-k)*n^k=  *1*(1-1/n)*(1-2/n)…*(1-
*1*(1-1/n)*(1-2/n)…*(1- 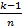 )* (pn*n)^k * (1-pn)^k * (1-pn)^ (-k) =
)* (pn*n)^k * (1-pn)^k * (1-pn)^ (-k) =  * 1*(1-1/n)*…*(1-
* 1*(1-1/n)*…*(1- 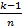 )*
)* 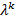 * (1-𝜆/n)^n * (1-𝜆/n)^(-k) (Первые две скобки при n
* (1-𝜆/n)^n * (1-𝜆/n)^(-k) (Первые две скобки при n 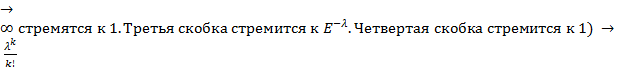 *
* 
 (
(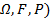
Опр: Случайной величиной X:𝛺  (
(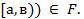
Пример:
𝛺= 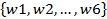
X1: X1(Wi)=  (скобка квадратная!)
(скобка квадратная!)
X2: X2(Wi) =  (скобка квадратная!)
(скобка квадратная!)
X3: X3(Wi)=i
15. Распределение, функция распределения. Свойства функции распределения.
Распределение – это закон, который описывает область значений случ вел и вероятность их исхода.
Опр: функция распределения случ вел Х это Fx:R 
Свойства:
1) 0 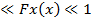
2) Fx(x)- неубывающая.
Док-во:
пусть 
Fx(y)=P(x 
3) Fx(x)- непрерывная слева
4) Fx(x) 
5) P(a 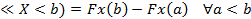
16. Случайные величины с дискретным распределением. Примеры.
Х- случ вел с дискретным законом распределения, если Х принимает конечное или счетное число значений.
* пусть а1,а2- все возможные значения случ вел х. р1,р2-соответсвующие вероятности. То есть pк это есть вероятность события, что x принял значение a с номером К. Т.е. pk=P(X=ak)=P(w:X(w)=ak)
Свойства чисел pk:
1) pk 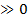
2) 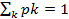
Примеры:
1) Х: С
Р: 1
Случ вел с вырожденным в т.С распределением.
2) Х с распред. Бернулли с параметром р (0<p<1)
X: 0, 1 P(X=1)=p
P: 1-p, pP(X=0)=1-p
3) Случ вел Х с биномиальным распред. c параметром p и n (n-натуральное число, 0 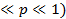
X: 0,1,2…n и pk=P(X=k)=Cn^k*p^k*(1-p)^(n-k)
4) X с распред Пуассона с параметром 𝜆 
X: 0,1,2,…и pk=P(X=k)= 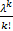 *
* 
5) X с геомтрраспред с параметром р (0<p<1)
X: 0,1,2…и pk=P(X=k)=((1-p)^k)*p
17. Случайные величины с абсолютно непрерывным распределением. Плотность распределения и ее свойства. Примеры непрерывных законов распределения.
Опр: Х-случ вел с абснепрерывраспред, если существует такая функция р(х),такая что для любого вещественного числа у
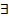 p(x):
p(x): 
Fx(y) = 
p(x) = px(x)- плотность распределения случ вел Х.
Свойства плотности:
1) px(x) 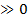 т.к. px(x)=F’x(x)
т.к. px(x)=F’x(x) 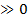
2) 
Примеры:
1) Х с равномерным распред на [a;b], (a<b)
px(x)= 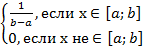
2) Случ вел Х с экспоненциальным распред с парам 𝞪>0
px(x)= 
Fx(x)= 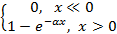
3) X с нормальным (гауссовским) распред с парам. a, 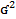 (a
(a 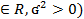
X 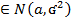
px(x)=  *
* 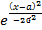
3’) a=0, 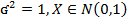
X- со станд нормой распр
px(x)= 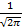 *
*  = 𝞿(х)
= 𝞿(х)
Fx(y)= 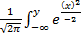 dx=Ф(y)
dx=Ф(y)
4) Случ вел с распр Коши
px(x)= 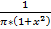
Fx(x)= 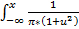 du
du
18. Случайные векторы. Совместная функция распределения.
(𝛺,F,P)
X:𝛺 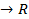
Fx:R 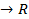
X1,X2,…Xn- случ вел
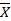 =(X1,…Xn):𝛺
=(X1,…Xn):𝛺  -случ вектор
-случ вектор
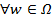
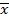 (w)=(X1(w),X2(w),…,Xn(w))
(w)=(X1(w),X2(w),…,Xn(w))
F 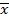 :
:  – функция распр случ вектора
– функция распр случ вектора
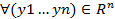 Fx(y1…yn)=P(x1<y1,…xn<yn)- совместная функция распред.
Fx(y1…yn)=P(x1<y1,…xn<yn)- совместная функция распред.
19. Свойства совместной функции распределения.
1) 0  (y1,…yn)
(y1,…yn) 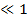
2) Если x1<y1 и x2<y2,…,xn<yn, то  (x1,…xn)
(x1,…xn)  (y1,…,yn)
(y1,…,yn)
3)  (x1…xk…xn) при xk
(x1…xk…xn) при xk 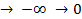
4)  (x1…xk…xn) при xk
(x1…xk…xn) при xk 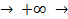 F(x1,xk-1,xk+1,..,xn)(x1,xk-1,xk+1,..,xn)
F(x1,xk-1,xk+1,..,xn)(x1,xk-1,xk+1,..,xn)
5)  (x1…xn) при x1
(x1…xn) при x1 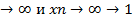
6) (n=2) a1<b1, a2<b2
P(a1  F(x1,x2)(b1b2)-F(x1,x2)(a1b2)-F(x1,x2)(b1a2)+F(x1,x2)(a1a2)
F(x1,x2)(b1b2)-F(x1,x2)(a1b2)-F(x1,x2)(b1a2)+F(x1,x2)(a1a2)
20. Независимость случайных величин.
Опр: X и Y- независимые сл.в., 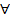 x, y
x, y 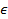 R
R
F (x,y) (X,Y) =F x (X)*F y (Y)
P (X<x, Y<y) = P (X<x)*P(Y<y)
Опр: X, Y-незав.сл.вел. ó 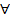 a1<b1 и a2<b2
a1<b1 и a2<b2
P(X 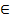 [a1,b1), Y
[a1,b1), Y 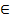 [a2,b2)) = P (X
[a2,b2)) = P (X 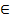 [a1,b1))*P (Y
[a1,b1))*P (Y 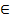 [a2,b2))
[a2,b2))
Доказательство:
P (X 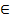 [a1,b1), Y
[a1,b1), Y 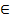 [a1,b2)) = P(X
[a1,b2)) = P(X 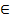 [a1,b1))*P (Y
[a1,b1))*P (Y 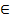 [a2,b2))
[a2,b2))
Левая часть верхнего равенства при a1à - 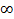 и при a2à -
и при a2à - 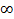 СТРемится к P (X<b1, Y<b2)
СТРемится к P (X<b1, Y<b2)
Правая часть - все тоже самое.
Левая часть: F (x,y) (b1,b2) = правой части Fx(b1)*Fy(b2)
21. EX (матем.ожидание) и свойства.
(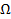 , F, P) X- случ.вел
, F, P) X- случ.вел
X- с дискретным распред.
Матем.ожиданиесл.вел.X называют число EX=  ai *pi, если это число существует. Если ряд расходитсàEX нет
ai *pi, если это число существует. Если ряд расходитсàEX нет
X- с непрерывным зак.распр. (px(x)-плотность)
Матем.ожид.сл.вел. X называют число EX=  dx, если это число сущ. Если интеграл расходится àEX нет
dx, если это число сущ. Если интеграл расходится àEX нет
Свойства:
Если P(X=c)=1,то EX=c
Если X, Y-случ.вел.,  ,
,  R
R
E( )=
)= 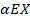 +
+ 
Если P(x>0)=1, то EX>=0
Если P(X>=Y)=1, то EX=EY
P (X>=Y)=P(X-Y>0)=1 => E(X-Y)=0 => EX-EY=0 =>EX=EY
|EX|<=E|X|
|X|>=x
|X|>=-x из этих двух условий следует E|X|>=EX и E|X|>=-EX
E|X|>= |EX|
Если X и Y-незав.сл.вел., то E(XY)=EX*EY, но не наоборот
Пусть f-функция (f:RàR), тогда а) если X с абсол.непр.распр, то Ef(x)= 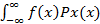 dx
dx
Б) с дискретным расп. Ef(x)= 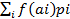
 2021-10-20
2021-10-20 100
100








