31Несмещенные, состоятельные, асимптотически нормальные оценки.
1. 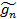 - несмещенная оценка, если E
- несмещенная оценка, если E 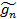 = Ɵ. Асимпт несмещ, если E
= Ɵ. Асимпт несмещ, если E 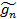 → Ɵ, где n→0.
→ Ɵ, где n→0.
2. 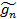 – состоятельная оценка, если ∀
– состоятельная оценка, если ∀ 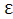 >0 P(|
>0 P(| 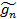 - Ɵ|≥
- Ɵ|≥ 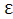 )→0 n→беск, P(|
)→0 n→беск, P(| 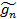 - Ɵ|< ε)→1 n→беск𝕝(-беск,t)
- Ɵ|< ε)→1 n→беск𝕝(-беск,t)
3. 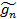 – асимтотич норм cдисп
– асимтотич норм cдисп 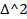 , если ∀t∈RP(
, если ∀t∈RP(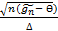 <t)→ Ф(t)=1/
<t)→ Ф(t)=1/  *
*  du
du
32Свойства выборочной функции распределения
 (t) – несмещ оценка для F(t)-генерфункраспр, то есть E
(t) – несмещ оценка для F(t)-генерфункраспр, то есть E  (t)=F(t) Док-во: Fn(t)=1/n
(t)=F(t) Док-во: Fn(t)=1/n 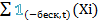
1 (-беск,t) (Xi)={1, Xi<t 0, Xi≥t}
P(𝕝(-беск,t) (Xi)=1)=P(Xi<t)=F(t) 1 (-беск,t) (Xi): 0 – 1-F(t); 1 – F(t) 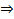 E
E 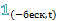 (Xi)=F(t)
(Xi)=F(t)
E  (t)=E 1/n
(t)=E 1/n 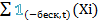 =1/n
=1/n 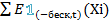 =F(t)
=F(t)  несмещ
несмещ
Теорема Гливенко
 (t) – состоят оценка для F(t)
(t) – состоят оценка для F(t)
 (t) = 1/n
(t) = 1/n  (Xi) по теореме Хинчина о ЗБЧ P(|1/n
(Xi) по теореме Хинчина о ЗБЧ P(|1/n  (Xi) – F(t)|≥
(Xi) – F(t)|≥ 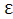 →0 n→беск)
→0 n→беск)  состоят.; 1/n
состоят.; 1/n  (Xi) =
(Xi) =  (t)
(t)
33Свойства выборочного мат ожидания
1. 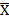 является несмещ и состоят оценкой для неизвестн мат ожидания a
является несмещ и состоят оценкой для неизвестн мат ожидания a
2. Если сущ-етG^2=DX, то 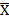 – асимпт норм оценка для a
– асимпт норм оценка для a
Доказательство:
1. Несмещ: E 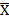 =E1/n
=E1/n 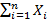 =1/n
=1/n 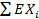 =а
=а
Состоят: ∀ 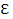 >0 P(|E1/n
>0 P(|E1/n 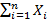 – a|≥
– a|≥ 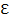 ) n→беск →0 – из теории Хинчина о ЗБЧ
) n→беск →0 – из теории Хинчина о ЗБЧ
2. ассимп норм: ∀t 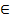 RP(
RP(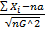 <t) → Ф(t) – по цпт Леви.
<t) → Ф(t) – по цпт Леви. 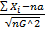 =
= 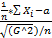 =
= 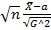
Свойства выборочной дисперсии
1. Статистика S^2 не завис от сдвига выборки
2.Статистика S^2 явл асимптот несмещ и состоят оценкой для G^2
Доказательство:
1. 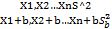 доказать
доказать 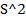 =
= 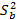
Док-во 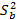 = 1/n
= 1/n 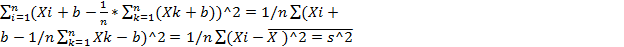
2. X1-EXi= 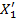 , X2-EXi=
, X2-EXi=  … Xn-EXi=
… Xn-EXi= 
Es^2 = E1/n 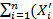 -
- 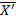 )^2 = 1/n
)^2 = 1/n 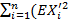 -
-  ) = 1/n
) = 1/n 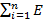 (Xi-EXi) =
(Xi-EXi) =
= E 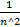 (
(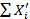 )^2=G^2 -
)^2=G^2 - 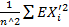 – 1/n
– 1/n  = G^2 - 1/n * G^2 =
= G^2 - 1/n * G^2 =  *G^2 n→0 →G^2
*G^2 n→0 →G^2
Состоятельность:
∀ 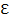 >0 P(|S^2-G^2| ≥
>0 P(|S^2-G^2| ≥ 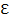 → 0
→ 0
P(|1/n 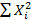 -
- 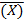 ^2-G^2| ≥
^2-G^2| ≥ 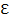 ), где G^2=E
), где G^2=E 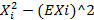
По ЗБЧ Хинчина: 1/n 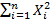 ~EXi^2
~EXi^2
По сво йствам 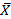 :
:  ~(EXi)^2
~(EXi)^2
34Распределение Хи-квадрат и Стьюдента. Лемма Фишера.
1. распред хи-кв с n степенями свободы
Y1,Y2…Yn – независодинакраспрс.в. Yk∈N(0,1)
 ^2=
^2=  – распред по зак хи-кв с n степ свободы (числослагаем)
– распред по зак хи-кв с n степ свободы (числослагаем)
2. Распр Стьюдента с n степенями свободы
Y0,Y1…Yn – независ од распр с. в., Yk∈N(0,1)
Tn= 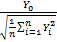 - с.в. распред по зак Стьюдента с n степенями свободы
- с.в. распред по зак Стьюдента с n степенями свободы
3. Лемма Фишера
1)  *
* 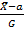 ∈N(0,1) – статистика имеет станд норм закраспр
∈N(0,1) – статистика имеет станд норм закраспр
2) 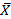 , s^2 – независс.в.
, s^2 – независс.в.
3) 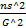 распр по зак
распр по зак 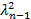 ((n-1)-степ своб)
((n-1)-степ своб)
4) 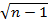 *
* 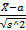 имеетраспр Стьюдента с (n-1) степ своб
имеетраспр Стьюдента с (n-1) степ своб
 2021-10-20
2021-10-20 93
93








