22. Примеры вычисления EX (матем.ожид) для двухточечного, биномин., пуассоновского, равномер и нормального распред.
1)(двухточ) X 0, 1
P 1-p, p
EX=0*(1-p)+1*p=p
2)(бином) X 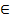 B(n,p) EX=np
B(n,p) EX=np
X: 0,1,2,…n
P(X=k)= 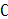 n^k p^k (1-p)^(n-k)
n^k p^k (1-p)^(n-k)
Или вот так: Yi0, 1
1-p, p
X= 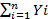 EX=E(
EX=E(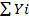 )=
)= 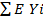 = np
= np
3)(Пуассон) X: 0, 1, 2, …
X 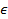 П
П  Pk=P(X=K)=
Pk=P(X=K)= 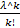 * e^ (-λ)
* e^ (-λ)
EX =  =
=  *e^(-λ) = e^(-λ) *
*e^(-λ) = e^(-λ) * 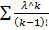 = e^(-λ) *λ*
= e^(-λ) *λ* 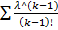 = |k-1=L| = =e^(-λ)*λ*
= |k-1=L| = =e^(-λ)*λ* 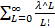 = λ
= λ
4)(абсол.непрер.)(равном) X 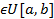 Px(𝑥)=
Px(𝑥)= 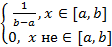
EX = 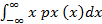 =
= 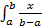 dx =
dx = 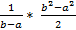 =
= 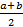
5)(нормаль.закон) X 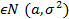
Px(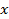 ) =
) = 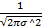 * e ^ (-
* e ^ (- 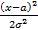 )
)
EX = 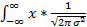 * e ^ (-
* e ^ (- 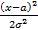 ) dx =
) dx = 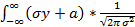 * e^(-
* e^(- 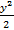 )*
)* 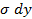 =
= 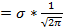 *
* 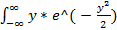 dy + a *
dy + a * 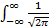 * e ^ (-
* e ^ (- 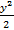 ) dy = a
) dy = a
Левая часть последнего равенства = 0,тк нечетная функция. Правая часть =1, тк четная
23. Дисперсия и ее свойства.
Дисперсия случ.велX называют число DX = E(X-EX)^2
Свойства:
DX>0
DX=0 ó 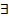 a: P (X=c)=1
a: P (X=c)=1
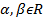 =>D((
=>D((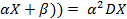
D(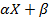 ) = E (
) = E (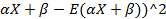 = E(
= E(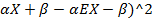 = E
= E 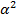 (X-EX)^2 =
(X-EX)^2 = 
DX=EX^2 – (EX)^2
DX=E(X-EX)^2 = E(X^2-2*X*EX+ (EX)^2))= EX^2-2*EX*EX+EX^2 = EX^2 – (EX)^2
X и Y-независ.сл.вел
D(X+Y)=DX+DY
D(X+Y) = E(X+Y-E(X+Y))^2 = E(X+Y-EX-EY)^2 = E((X-EX)^2+(Y-EY)^2 + 2(X-EX)(Y-EY)) = =E(X-EX)^2 +E(Y-EY)^2+ 2E(X-EX)(Y-EY) = DX+DY+2E(X-EX)(Y-EY) = DX+DY
24. Примеры вычисления дисперсий для различных распределений.
1) X: c= 1 => DX=0
2) X: 0, 1
1-p, p =>DX=EX^2 – p^2 = p-p^2 =p(1-p)
X^2: 0, 1
1-p, p =>EX^2=p
X 
Y1,Y2,…Yn – независ.случ.вел
Yk: 0, 1
1-p, p
X= 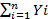 , DX=D(
, DX=D(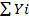 ) =
) = 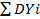 = np(1-p)
= np(1-p)
X 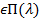 X: 0,1,2,… pk=p(X=k)=
X: 0,1,2,… pk=p(X=k)= 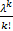 * e^(-λ)
* e^(-λ)
EX = 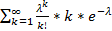 = λ*e^(-λ)
= λ*e^(-λ) 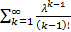 = λ
= λ
EX^2 = 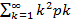 =
= 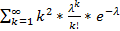 =
= 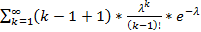 =
=  +
+ 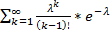 = λ^2*e^(-λ)
= λ^2*e^(-λ) 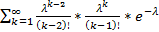 + λ*e^(-λ)
+ λ*e^(-λ) 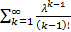 = λ^2+λ
= λ^2+λ
DX = λ^2+λ-λ^2 = λ
(непрер) X 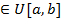
Px(𝑥) = 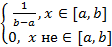
EX= 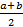 . EX^2=
. EX^2= 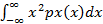 =
=  =
= 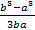
DX= 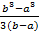 -
- 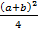 =
= 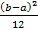
X 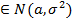 – нормал.закон
– нормал.закон
Px(𝑥) =  . EX=a
. EX=a
DX= 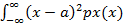 =
=  = |y=
= |y= 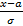 | =
| = 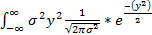 *
* 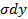 =
= 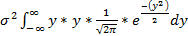 =
= 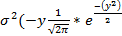 )| (сверху
)| (сверху 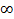 , снизу -
, снизу - 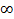 ) +
) + 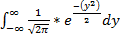 =
= 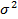
25. Моменты случайных величин
k>=0 –целое число
Моментом k-ого порядка случ.велX называют число EX^k, если это число существует
Централь.момент. k-ого порядка сл.вел. X называют E(X-EX)^k
Абсолют.моментE|X|^k
26. Ковариация и коэффициент корреляции. Свойства коэффициента корреляции
1. cov (X,Y) = E(X-EX)(Y-EY)
2. X, Y – случ.вел., сущ. DX>0, DY>0. 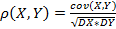
Свойства коэф.коррел.:
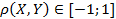
| 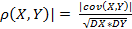 =
= 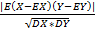 =<
=<  =<
=< 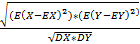 = 1
= 1
X,Y- незав.случ.вел => 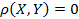
Cov(X,Y)= E(X-EX)(Y-EY) = E(X-EX)E(Y-EY)=0*0=0
Пусть 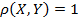
D (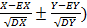 = E
= E 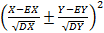 = E
= E 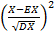 + E
+ E 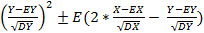 = 1+1+- 2*
= 1+1+- 2* 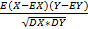 = 2+-2
= 2+-2 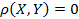 ó сущ. C
ó сущ. C 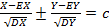 óY=
óY= 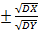 *x + b
*x + b
27. Неравенства Маркова и Чебышева.
1. Неравенство Маркова. X принимает неотрицательные знач. Тогда 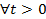 P(X>=t)=<
P(X>=t)=< 
Док-во: для дискретн.распред.X
X: a1, a2,…
P1, p2,…
EX = 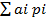 =
= 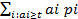 +
+ 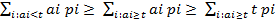 = t
= t 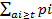 = t*p(x>=t)
= t*p(x>=t)
2. Нер-во Чебышева
X – случ.вел. a=EX, 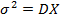 тогда
тогда 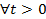
P(|X-a|>= t) =< 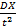
Док-во: P(|X-a|>=t) = P ((x-a)^2 >= t^2) =< 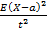 =
= 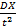
 2021-10-20
2021-10-20 65
65








