28. ЗБЧ. Теоремы: Чебышев и Хинчин.
Опр: X1, X2,.. –послед-тьслуч.вел, ak=EXk, для этой послд-ти выполняется ЗБЧ, если 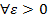
P (| 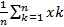 -
- 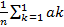 | >=
| >= 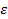 ) à 0 при n->
) à 0 при n-> 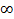
Чебышев:
X1,X2,…-независ.случ.век
Ak=EXk,  =DXk. сущC>0:
=DXk. сущC>0: 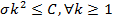
Док-во: 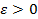 P(|
P(| 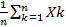 -
- 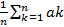 |>=
|>= 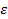 ) = P (|
) = P (| 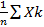 - E
- E 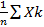 |>=
|>= 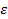 ) =<
) =< 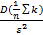 =
= 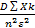 =
= 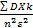 =<
=< 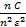 à 0 при nà
à 0 при nà 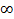
Хинчин: X1, X2,…-незав.случ.вел.,одинаковораспред., a=EXk, тогда выполняется ЗБЧ
P(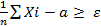 ) à 0 при nà
) à 0 при nà 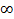
29Центральная предельная теорема. Теорема Леви.
Х1, Х2… - независодинакраспределс.в., а=ЕХk
G^2=DXk>0. Тогда ∀x∈R. P( <x)n→беск →Ф(х)=1/
<x)n→беск →Ф(х)=1/  *
* 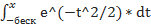
30Случайная выборка.
Х1, Х2…Хn ~ F(x) – случ. Выборка, объема n. Независ, одинак. распред. и вел.
Статистика или оценка.
Рассм. ф-ю д.:R^n → R. д(Х1,Х2…Хn)= 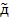 n – функция от случ выборок
n – функция от случ выборок
Выборочная ф-я распределения.
Fn(t)= (число тех Xi<t)/n =1/n * 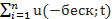 (Xi),
(Xi),
где 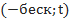 -Uα(x) – индикатор множества А
-Uα(x) – индикатор множества А
Uα(х) = 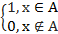
Выборочные моменты.
Пусть k≥1 Ak=1/n * 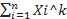 – выбороч моменты k-го порядка.
– выбороч моменты k-го порядка.
αk=1/n 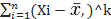 – центр выб моменты k-го порядка
– центр выб моменты k-го порядка
Порядковые статистики.
Построим вариат ряд X1, X2…Xn. X1=min(X1…Xn) – min пор стат
X2=…след знач…Xk к-я поряд стат. Xn = max(X1…Xn) – max пор стат
Вариационный ряд.
Упорядоченная по величине послед-ть выборочных значений наблюдаемой величины. X(n+1)/2
Выборочные квантили.
0<α<1 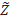 α=X[αn]+1– выб квантиль порядка α
α=X[αn]+1– выб квантиль порядка α
([an] – целая часть)
Медиана выборки.
– выб квантиль порядка α=1/2. 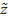 1/2 =
1/2 =  1/2 =
1/2 = 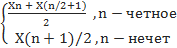
Выборочная cov ковариация.
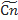 (X,Y) = 1/n
(X,Y) = 1/n 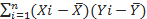
Выборочный коэф корреляции.
Rn(X,Y)= 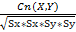 , где S^2=1/n
, где S^2=1/n 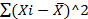
 2021-10-20
2021-10-20 80
80








