Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной.
Формула для расчета средней гармонической простой будет иметь вид:
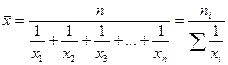
Формулу для расчета средней гармонической взвешенной можно представить в общем виде:
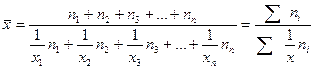
Например, имеются следующие данные:
| Выпуска продукции, тн. | Производительность труда, тн./чел.-час | |
| Цех 1 | ||
| Цех 2 | ||
| Итого |
Необходимо определить среднюю производительность труда. Для решения этой задачи необходимо пользоваться средней гармонической взвешенной:
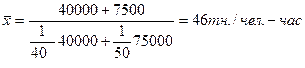
Средняя хронологическая применяется для оценки среднего уровня ряда динамики. При наличии информации на моменты времени с равными интервалами между ними используется средняя хронологическая простая:
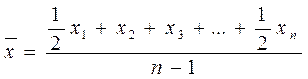 , где
, где
n – число моментов (дат)
Средняя геометрическая применяется, как правило, для оценки среднего показателя относительных величин (например, средний темп роста).
Средняя геометрическая простая определяется по формуле:
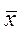
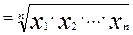
Средняя геометрическая взвешенная определяется по формуле:
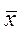
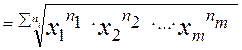
Средняя квадратическая применяется для определения средних размеров диаметров труб стальных, стволов деревьев и т.д. Этот вид средней также используется при расчете показателей вариации
· простая:
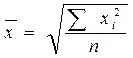
· взвешенная:
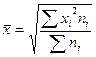
При расчете различных степенных средних по одним и тем же данных статистического наблюдения средние не буду одинаковы. Чем выше степень k средней, тем больше ее величина. Математически доказано, что между величинами степенных средних, рассчитанных по одной и той же совокупности единиц статистического наблюдения и одному и тому же признаку, существует следующее соотношение:
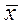 гарм <
гарм < 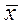 геом <
геом < 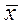 ар <
ар < 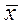 кв.
кв.
 2014-02-13
2014-02-13 2126
2126








