В о
Если мы имеем чертеж с изображением отрезка в двух проекциях, то имеются все геометрические элементы для определения натуральной величины отрезка. Восстановим перпендикуляр к проекции А 1В 1 и на нем отложим расстояние равное В 2 1 2. Полученную точку В о соединим с горизонтальной проекцией А 1 точки А. Полученная гипотенуза будет натуральной величиной отрезка прямой АВ, а угол a будет натуральным углом наклона данного отрезка к горизонтальной плоскости проекций.
Без нахождения натуральной длинны отрезка нельзя найти угол наклона прямой к плоскости проекций. Поэтому если требуется найти углы наклона прямой ко всем плоскостям проекций (П 1, П2, П 3), то необходимо определить натуральную длину отрезка на всех плоскостях проекций.
При подготовке к практическому занятию решите этим методом задачу 9 из Тетради.
Рассмотрим частные случаи расположения прямой в пространстве относительно плоскостей проекций.
Это прямые параллельные плоскостям проекций.
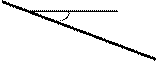
Пряма параллельная горизонтальной плоскости проекций называется горизонтальной прямой уровня или горизонталью и обозначается h.
Все точки этой прямой находятся на одинаковом расстоянии от горизонтальной плоскости проекций (на одном уровне) и поэтому ее легко узнать на чертеже - фронтальная проекция этой прямой всегда параллельна оси Х 1,2, горизонтальная проекция отрезка этой прямой равна его натуральной величине.
ê А 1В 1ê= ê А,В ê, êb 1 ê=êb ê; -угол наклона горизонтали к плоскости П 2 (фронтальной плоскости).




А 2 h 2 В2
Х 1,2
 |
А1 b 1
h 1 В 1
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой уровня или фронталью (f). Горизонтальная проекция фронтали параллельна оси проекций Х 1,2. Все точки фронтали находятся на одинаковом расстоянии от фронтальной плоскости проекций. Длинна фронтальной проекции отрезка фронтали равна его натуральной величине, а угол наклона фронтали к плоскости П 1 равен фронтальной проекции этого угла:
В 2

 f 2
f 2
 А 2 a 2
А 2 a 2
 |
Х 1,2

f 1
 А1 В 2
А1 В 2
çА2, В2 ç= çА, Вç, а угол a = çf, П1ç = ç a 2 ç
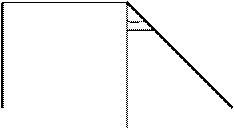
Прямая параллельная профильной плоскости проекций, называется профильной прямой уровня. Горизонтальная (р 1) и фронтальная (р 2) проекции профильной прямой перпендикулярны оси проекций Х 1,2. Длина профильной проекции отрезка прямой равна его натуральной величине. Углы наклона к плоскостям проекций профильной проекции равны их натуральной величине.
êА з, В з ê = êА,В ê, êa з ê= êa ê, êb з ê = êb ê.
 В 2 В з
В 2 В з
 |
р 2 b з р з
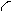 А 2 a з А з
А 2 a з А з


 Х 0 Y
Х 0 Y
 |
 B 1
B 1

 A 1
A 1
Y
 2014-02-09
2014-02-09 1277
1277








