Рассмотрим некоторый линейный оператор 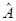 :
: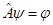 . Выберем в рассматриваемом линейном пространстве дискретный ортонормированный базис. Так как каждому элементу этого пространства соответствует набор его координат в выбранном базисе, то оператору
. Выберем в рассматриваемом линейном пространстве дискретный ортонормированный базис. Так как каждому элементу этого пространства соответствует набор его координат в выбранном базисе, то оператору 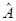 соответствует закон, связывающий координаты элементов линейного пространства. Можно доказать, что для любого линейного оператора закон, позволяющий найти координаты элемента
соответствует закон, связывающий координаты элементов линейного пространства. Можно доказать, что для любого линейного оператора закон, позволяющий найти координаты элемента 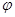 по координатам элемента
по координатам элемента 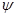 , можно представить в виде произведения некоторой матрицы из чисел на столбец, составленный из координат
, можно представить в виде произведения некоторой матрицы из чисел на столбец, составленный из координат 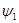 ,
, 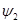 ,
, 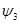 , … элемента
, … элемента 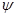
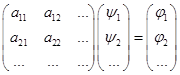 (1)
(1)
где под умножением матрицы на столбец понимается принятое в линейной алгебре правило матричного умножения («строка на столбец»):
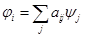 (2)
(2)
Числа 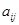 , которые являются характеристикой оператора, но не зависят от элемента
, которые являются характеристикой оператора, но не зависят от элемента 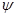 , составляют матрицу оператора
, составляют матрицу оператора 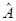 . Очевидно, размерность матрицы оператора совпадает с размерностью пространства, в котором оператор действует. В частности, операторам, действующим в бесконечномерных пространствах отвечают бесконечные матрицы.
. Очевидно, размерность матрицы оператора совпадает с размерностью пространства, в котором оператор действует. В частности, операторам, действующим в бесконечномерных пространствах отвечают бесконечные матрицы.
Можно доказать, что сумме и произведению операторов отвечает сумма и произведение их матриц:
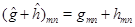
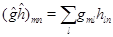 (3)
(3)
Матричные элементы матрицы оператора можно связать с результатом его действия на базисные элементы. Действительно, пусть 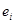 - ортонормированный базис. Разложим элементы
- ортонормированный базис. Разложим элементы 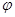 и
и 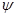 в определении оператора
в определении оператора 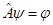 по базису
по базису 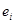 :
:
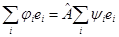 (4)
(4)
где 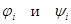 - координаты элементов
- координаты элементов 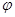 и
и 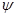 . Умножим скалярно равенство (4) на
. Умножим скалярно равенство (4) на 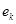 и, пользуясь ортонормированностью базиса, линейностью оператора и скалярного произведения, получим
и, пользуясь ортонормированностью базиса, линейностью оператора и скалярного произведения, получим
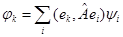 (5)
(5)
Сравнивая (4) с определением матрицы оператора, заключаем, что
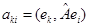 (6)
(6)
Из формулы (6) можно получить ряд следствий.
1. Если в качестве базиса выбрать собственные функции оператора, его матрица является диагональной
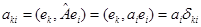 (7)
(7)
причем на диагонали размещаются собственные значения оператора 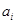 .
.
2. Матрицы сопряженных операторов транспонированы и комплексно сопряжены друг по отношению к другу:
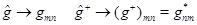 (8)
(8)
3. При комплексном сопряжении и транспонировании матрицы эрмитова оператора получается та же матрица
если 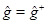 то
то 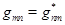 (9)
(9)
4. При изменении базиса матрица изменяется. Остановимся на этом пункте более подробно. Пусть выбрано два ортонормированных базиса 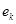 и
и 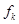 . Каждый базисный элемент
. Каждый базисный элемент 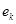 можно разложить по базису
можно разложить по базису 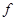 :
:
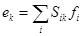 (10)
(10)
где 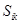 - некоторые числа, которые образуют квадратную матрицу (удобнее выполнять суммирование по первому индексу матрицы
- некоторые числа, которые образуют квадратную матрицу (удобнее выполнять суммирование по первому индексу матрицы 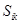 - так, как это сделано в (10)). Матрицу
- так, как это сделано в (10)). Матрицу 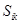 принято называть матрицей перехода от одного базиса к другому. Очевидно, матрица перехода от одного ортонормированного базиса к другому является унитарной. Действительно, из ортонормированности обоих базисов имеем
принято называть матрицей перехода от одного базиса к другому. Очевидно, матрица перехода от одного ортонормированного базиса к другому является унитарной. Действительно, из ортонормированности обоих базисов имеем
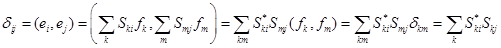 (11)
(11)
Но так как 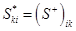 , из (11) имеем
, из (11) имеем
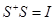 (12)
(12)
где 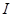 - единичная матрица, что и означает, что матрица перехода унитарна (равенство (12) есть определение унитарного оператора).
- единичная матрица, что и означает, что матрица перехода унитарна (равенство (12) есть определение унитарного оператора).
Чтобы установить связь между матрицами одного и того же оператора при разных выборах базиса воспользуемся формулой (7) и формулой связи базисов
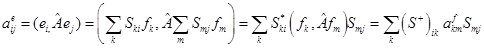 (13)
(13)
где 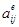 и
и 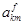 - матрицы оператора
- матрицы оператора 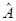 в базисе
в базисе 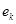 и
и 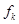 соответственно. С помощью правил матричного умножения формулу (13) можно записать в виде
соответственно. С помощью правил матричного умножения формулу (13) можно записать в виде
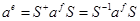 (14)
(14)
Из формулы (14), в частности, следует, что шпур матрицы оператора (сумма диагональных элементов) не зависит от выбора базиса или, как говорят, является инвариантным относительно выбора базиса (это связано с тем, что если под знак шпура входит произведение матриц, матрицы в нем можно циклически переставлять). Поэтому при любом выборе базиса шпур матрицы эрмитового оператора равен сумме его собственных значений. Также инвариантным является детерминант матрицы оператора.
Исследуем теперь вопрос о существовании общих собственных функций у разных операторов. Справедлива следующая
теорема:
Для того чтобы два оператора 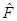 и
и 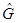 имели полную систему общих собственных функций необходимо и достаточно, чтобы они коммутировали:
имели полную систему общих собственных функций необходимо и достаточно, чтобы они коммутировали: 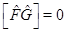 .
.
Необходимость: Пусть 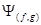 - полная система общих собственных функций. Тогда любую функцию
- полная система общих собственных функций. Тогда любую функцию 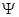 можно разложить по
можно разложить по 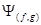 :
: 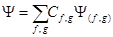 . Подействуем на это равенство коммутатором
. Подействуем на это равенство коммутатором
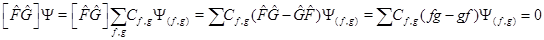 (15)
(15)
где 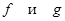 собственные значения. Так как
собственные значения. Так как 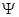 произвольна, то
произвольна, то 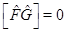 .
.
Достаточность: 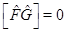 . Подействуем на уравнение на собственные функции оператора
. Подействуем на уравнение на собственные функции оператора 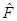
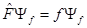 (16)
(16)
где 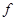 ,
, 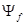 - собственное значение и собственная функция оператора
- собственное значение и собственная функция оператора 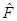 , оператором
, оператором 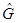
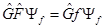 (17)
(17)
Благодаря коммутации операторов и линейности оператора 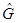 , имеем из (17)
, имеем из (17)
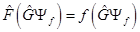 (18)
(18)
Таким образом, функция 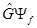 также является собственной для оператора
также является собственной для оператора 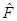 . Если у оператора
. Если у оператора 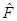 невырожденный спектр, то собственному значению
невырожденный спектр, то собственному значению 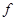 отвечает единственная собственная функция. Поэтому функция
отвечает единственная собственная функция. Поэтому функция 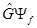 может отличаться от
может отличаться от 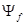 некоторым множителем:
некоторым множителем:
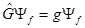 (19)
(19)
где буквой 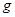 обозначен указанный множитель. Уравнение (19) и означает, что функция
обозначен указанный множитель. Уравнение (19) и означает, что функция 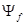 является собственной и для оператора
является собственной и для оператора 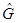 .
.
Если спектр оператора 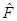 вырожден, то есть одному собственному значению отвечают несколько собственных функций, то функция
вырожден, то есть одному собственному значению отвечают несколько собственных функций, то функция 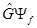 , вообще говоря, не сводится к функции
, вообще говоря, не сводится к функции 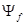 . В этом случае, однако, выбор собственных функций является неоднозначным и можно построить такие линейные комбинации собственных функций оператора
. В этом случае, однако, выбор собственных функций является неоднозначным и можно построить такие линейные комбинации собственных функций оператора 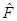 , которые будут также и собственными для оператора
, которые будут также и собственными для оператора 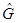 . Теорема доказана.
. Теорема доказана.
Так как операторы координаты и импульса не коммутируют, они не имеют полной системы общих собственных функций. На самом деле у этих двух операторов нет ни одной общей собственной функции. Поэтому нет состояний, в которых и координата и импульс одновременно имели бы определенные значения (именно поэтому в квантовой механике нет понятия траектории). Всегда существует либо разброс координат, либо разброс импульсов, либо и то и другое. Рассмотрим утверждение, связывающее эти величины и которое является одним из основополагающим законов квантовой механики.
Соотношение неопределенностей Гейзенберга.
Исходя из коммутатора оператора координаты и импульса
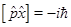 (20)
(20)
докажем, что
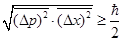
т.е. неопределенности координаты и импульса не могут быть одновременно уменьшены до сколь угодно малых величин.
Для доказательства рассмотрим произвольное состояние 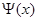 . Пусть в этом состоянии:
. Пусть в этом состоянии: 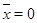 и
и 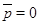 (этого всегда можно добиться выбором системы координат). Тогда:
(этого всегда можно добиться выбором системы координат). Тогда:
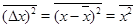
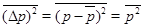 (21)
(21)
Рассмотрим некоторый функционал от действительной переменной 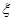 :
:
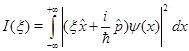 (22)
(22)
Очевидно, что 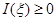 , как интеграл от четной неотрицательной функции. Учитывая, что x-действительная величина и что действие оператора координаты в собственном представлении сводится просто к умножению на значение координаты x, получим:
, как интеграл от четной неотрицательной функции. Учитывая, что x-действительная величина и что действие оператора координаты в собственном представлении сводится просто к умножению на значение координаты x, получим:
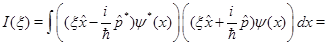
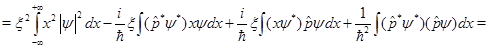
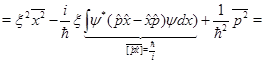
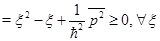 (23)
(23)
Полученное выражение как функция переменной 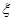 , представляет собой параболу с ветвями, направленными вверх. Чтобы выполнялось неравенство (23) при любых
, представляет собой параболу с ветвями, направленными вверх. Чтобы выполнялось неравенство (23) при любых 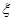 необходимо, чтобы
необходимо, чтобы 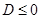 . Получим:
. Получим:
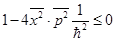 (24)
(24)
Или
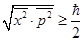
Поскольку 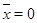 и
и 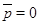 , то:
, то:
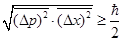
Мы получили точную формулировку соотношения неопределенностей Гейзенберга.
Замечание:
1. Если бы операторы 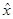 и
и 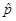 коммутировали, то мы не смогли бы получить этого соотношения.
коммутировали, то мы не смогли бы получить этого соотношения.
2. Состояние, которое «минимизирует» соотношение неопределенностей:
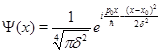
Это состояние представляет собой гауссовский волновой пакет. В нем:
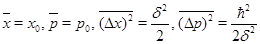
 2014-02-13
2014-02-13 1139
1139