Пусть дано поле R. тогда таблицу вида:
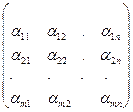 , где aik ÎR, называют матрицей порядка m´n и обозначают короче ||aik || i = 1, 2,..., n, k = 1, 2,...,m или буквами А, В, С,...
, где aik ÎR, называют матрицей порядка m´n и обозначают короче ||aik || i = 1, 2,..., n, k = 1, 2,...,m или буквами А, В, С,...
Любая строка этой матрицы есть n-мерный арифметический вектор, а любой столбец - m-мерный арифметический вектор.
Всю матрицу можно рассматривать как m´n -мерный вектор.
Множество всех матриц с элементами из поля R принято обозначать символом Mmn(R). На некоторых подмножествах этого множества можно определить две бинарные операции (+, ×) и две унарные операции (умножение матрицы на скаляр и нахождение обратной матрицы).
Операция сложения матриц определяется только для тех матриц из множества Mnm(R), которые имеют одинаковый порядок, т.е. одинаковое число строк и столбцов.
Если A = ||aik || и В=||bik ||, то А + В = С = ||aik + bik || i = 1, 2,... m, k= 1,2,...,n
Например, матрицы порядка 2´3 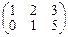 и
и 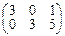 можно сложить и в результате получим матрицу:
можно сложить и в результате получим матрицу: 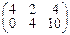 того же порядка 2x3, а матрицы вида:
того же порядка 2x3, а матрицы вида: 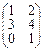 и (1 3 4 5) сложить нельзя, т.к. они имеют различный порядок.
и (1 3 4 5) сложить нельзя, т.к. они имеют различный порядок.
Операция умножения матриц определяется только для тех матриц из множества Mmn(R), порядки которых удовлетворяют следующему требованию: число столбцов первой матрицы должно совпадать с числом строк второй матрицы.
То есть, если матрица А имеет порядок m´n, то матрица В в произведении А × В должна иметь порядок n´s.
Тогда А • В = С = ||Cik ||. где Cik находится по правилу: i-ая строка матрицы А умножается на k-ый столбец матрицы В (в смысле скалярного произведения).
Например, если А = 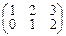 и В =
и В = 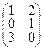 , то произведение А • В = С =
, то произведение А • В = С = 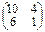
Найдем произведение В • А, это тоже можно сделать, так как число столбцов матрицы В совпадает с числом строк
матрицы А
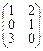 •
• 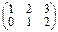 =
= 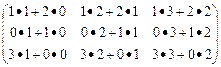 = =
= = 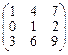
Замечания:
1. Как видим, А•В ¹ В•А, то есть операция умножения матриц некоммутативна.
2. Порядок матрицы А•В связан с порядками матриц А и В, матрица А•В имеет столько же строк, сколько и матрица А и столько же столбцов, сколько их имеет матрица В.
Матрицы 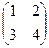 и
и 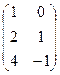 перемножить нельзя, так как их порядки не удовлетворяют требуемому условию.
перемножить нельзя, так как их порядки не удовлетворяют требуемому условию.
О перация умножения на скаляр определяется на всем множестве Mmn(R) без ограничений: l||aik ||=||laik ||
Пример 1: 3• 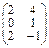 =
= 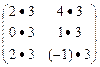 =
= 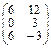
Определение 1. Нулевой матрицей называется квадратная матрица вида:
0 = 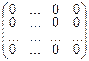 , у которой все элементы равны нулю.
, у которой все элементы равны нулю.
Проверьте самостоятельно, что если матрицы А и 0 одного порядка, то А+0 = 0+А = А т.е. матрица 0 играет роль нейтрального элемента на множестве Mmn(R), относительно операции сложения.
Определение 2. Матрица (-А) называется противоположной матрице А, если (-А) + А=А+(-А) = 0
Самостоятельно проверьте, что для матрицы А = 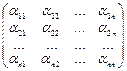 -А=
-А= 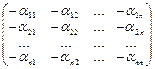
Теорема 1. Алгебра <Mnn(R), +> - аддитивная абелева группа.
Схема доказательства:
1. Множество Mnn(R) замкнуто относительно операции сложения матриц, т.к. "A, B Î Mnn(R), (A+B=C) Î Mnn(R) (смотри определение операции +).
2. "A, B, C Î Mnn(R), (A+B)+C = А+(В+С) т.к. операция сложения матриц определяется через операцию сложения действительных чисел, которая ассоциативна.
3. "A, B Î Mnn(R), А+В = В+А, т.к. операция сложения действительных чисел коммутативна.
4. $ нулевая матрица 0 = 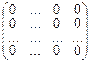 такая, что"A Î Mnn(R) 0 + А = А + 0 = А
такая, что"A Î Mnn(R) 0 + А = А + 0 = А
5. "A Î Mnn(R) $ (-A) = 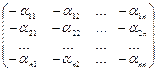 такая, что А + (-А) = (-А) + А = 0
такая, что А + (-А) = (-А) + А = 0
Итак. <Mnn(R), +> - абелева группа.
Определение 3. Единичной матрицей называется квадратная матрица вида:
E = 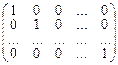 , у которой на главной диагонали стоят единицы, а все другие элементы равны нулю.
, у которой на главной диагонали стоят единицы, а все другие элементы равны нулю.
Проверьте самостоятельно, что если матрицы А и Е одного порядка, то А•Е=Е•А=А, т.е., что Е играет на множестве Mnn(R) роль нейтрального элемента по умножению.
Теорема 2. Алгебра <Mnn(R), +, •> - некоммутативное, ассоциативное кольцо с единицей и делителями нуля.
Для доказательства нужно проверить выполнимость всех условий в определении кольца:
1. Множество Mnn(R) замкнуто относительно операций, т.к.
"A, B Î Mnn(R), (A+B) Î Mnn(R) и (A•B) Î Mnn(R)
2. <Mnn(R), +> - абелева группа (см. теорему 1).
3. "A,B,CÎMnn(R), А•(В+С)=А•В+А•С, (В+С)•А= В•А+С•А.
4. "A, B, C Î Mnn(R), (A•B)•C = A•(B•C).
5. $ A, BÎMnn(R), A•B ¹ B•A.
6. $ E Î Mnn(R): "A, (E•A = A•E =A).
Каждую аксиому проверьте самостоятельно.
Покажем, что в кольце Mnn(R) есть делители нуля, например, если
А = 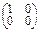 В =
В = 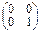 , то А•В =
, то А•В = 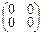
Понятно, что таких матриц одного и того же порядка существует множество.
Запишите самостоятельно такие матрицы третьего порядка.
Теорема 3. Алгебра <Mnn(R), +{wl|l Î R}> - линейное пространство размерности n´n.
Схема доказательства:
1-4) <Mnn(R), +> - абелева группа.
5) "A, B Î Mnn(R) "lÎR: l(A+B) = lA+lB.
6) "a, b Î R " AÎMnn(R): (a + b)A = aA + bA.
7) "a, b Î R " AÎMnn(R): (ab)•A = a(bA).
8) 1 • A = A.
Роль единичного базиса играет система матриц вида:
E1 = 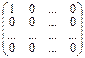 , E2 =
, E2 = 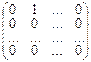 , En =
, En = 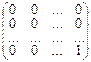
Наприм ер. В пространстве R22(R) матрица А = 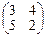 может быть разложена по единичному базису так:
может быть разложена по единичному базису так:
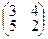 = 3
= 3 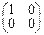 + 4
+ 4 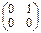 + 5
+ 5 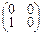 + 2
+ 2 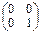
Определение 4. Ведущим (главным) элементом i-ой строки матрицы А называется первый отличный от нуля элемент этой строки.
Пример 2. А= 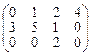 1 - ведущий элемент 1-ой строки, 3 - ведущий элемент 2-ой строки, 2 - ведущий элемент 3-ей строки.
1 - ведущий элемент 1-ой строки, 3 - ведущий элемент 2-ой строки, 2 - ведущий элемент 3-ей строки.
Определение 5. Матрица А называется ступенчатой, если:
1. под ведущими элементами каждой её строки стоят нулевые элементы.
2. нулевые строчки стоят последними.
Пример 3. А = 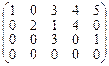 - ступенчатая матрица.
- ступенчатая матрица.
Определение 6. Элементарными преобразованиями матрицы называют следующие преобразования:
1. Перемена местами строк матрицы;
2. Умножение строки на число, отличное от нуля;
3. Прибавление к одной строке другой, умноженной на число, не равное нулю.
Если на множестве матриц Mnn(R), задать отношение j так: А j В Û (когда от А к В можно перейти с помощью элементарных преобразований), то это отношение будет отношением эквивалентности.
Действительно:
1. АÎ Mnn(R), А j А (очевидно).
2. "A, B Î Mnn(R), А j B => B j А (достаточно совершить преобразование в обратном порядке).
3. "A, B, C Î Mnn(R), (А j В) & (В j С) =>(А j С).
Если матрицы А и В эквивалентны, то будем записывать это так: А Û В.
Частным случаем этого отношения будет отношение А j В Û (А=В)
Определение 7. Если A = ||aik || и B = ||bik || i, k = 1...n, то А = В Û (aik = bik)
Теорема 4. Любую ненулевую матрицу A Î Mnn(R) можно привести к ступенчатому виду. Доказательство проведите самостоятельно методом математической индукции по числу строк матрицы.
Пример 4. В = 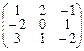 Û
Û 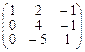 Û
Û 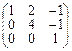
Первую строку матрицы умножили на 2 и сложили со второй строкой, затем снова первую строчку умножили на 3 и вычли из третьей строки, затем 2-ю строчку умножили на 5, 3-ю на 4 и сложили.
Определение 8. Строчным рангом ступенчатой матрицы называется число ее ненулевых строк. Обозначение: rang A = k. В примере 4 rang В = 3.
Определение 9. Матрица A = ||aik ||, где i, к = 1,2,..., n называется обратимой (невырожденной), если существует X Î Mnn(R): А•Х = Х•А = Е.
Докажем, что такая матрица (X) единственная для А.
Предположим противное, пусть существуют матрицы X и У, удовлетворяющие определению. Тогда (Х•А)•У=Х•(А•У) в силу ассоциативности операции умножения матриц.
Тогда: Е•У=Х•Е => (У=Х).
Матрицу X называют обратной матрицей к матрице А и обозначают А-1.
Теорема 5. Если квадратная матрица А порядка n´n обратима, то строчный ранг её ступенчатой матрицы равен n.
Доказательство: Так как матрица А обратима, то $А-1: А • А-1= Е (rang E=n) => (rang A=n). (Справедлива и обратная теорема. Докажите её самостоятельно).
Теорема 6. Любую обратимую матрицу A Î Mnn(R) с помощью элементарных преобразований можно привести к единичной матрице Е (т.е. матрица А эквивалентна единичной матрице Е).
Эта теорема является следствием теоремы 4.
Поэтому алгоритм нахождения обратной матрицы основан на том, что матрицы (А/Е) и (Е/А-1) - эквивалентны, и состоит в следующем:
1. К квадратной матрице А справа приписывается единичная матрица того же порядка, что и А, (А/Е);
2. С помощью элементарных преобразований от матрицы (А/Е) переходят к матрице (Е/А-1);
3. Записывают А-1 отдельно.
Замечание 1. В процессе нахождения обратной матрицы не обязательно проверять - обратима ли матрица, т.к. при элементарных преобразованиях сразу будет видно, имеет ли она обратную матрицу.
Пример 5. Найти обратную матрицу для матрицы
A = 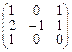 rang A=3 (проверьте), значит она обратима.
rang A=3 (проверьте), значит она обратима.
Найдем А-1
(А/Е) = 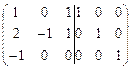 Û
Û 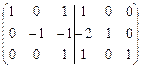 Û
Û 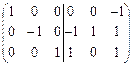 Û
Û 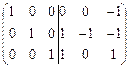 => A-1 =
=> A-1 = 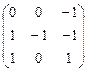
Проверка: А • A-1 = 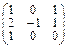
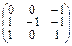 =
= 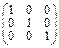
С помощью обратной матрицы можно решать матричныеуравнения, в которых роль переменной играет матрица X
Пример 6. Решить в общем виде уравнение. X • A + X = B
Решен ие.
Чтобы матрицу X можно было вынести за скобки, нужно представить слагаемое X =Е•Х, тогда Х•(А+Е) = В. Нельзя писать, что Х•(А+1) = В, т.к. А+1 не имеет смысла во множестве Rmn(R). Если матрица (А+Е) будет невырожденной, т.е. имеет обратную матрицу (А+Е)-1, то получим уравнение X (А+Е) (А+Е)-1 = В (А+Е)-1, т.к. умножение матриц некоммутативно, то в этом случае нужно умножать справа, тогда X • Е = В•(А+Е)-1 или Х = В•(А+Е)-1
Если матрица (А+Е) не имеет обратной матрицы, то исходное уравнение таким способом решать нельзя.
Пример 7. Решить матричное уравнение:
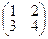 • X •
• X • 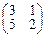 =
= 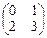
Решение.
1. Представим уравнение в виде А•Х•В = С
2. Выразим матрицу X: Х = А-1•С•В-1
3. Найдем А-1 и В-1:
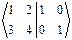 Û
Û 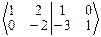 Û
Û 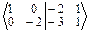 => A-1 =
=> A-1 = 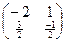
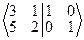 Û
Û 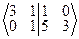 Û
Û 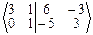 => B-1 =
=> B-1 = 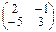 , тогда X =
, тогда X = 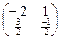 •
• 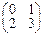 •
• 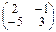 =
= 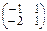
 2015-02-27
2015-02-27 4997
4997
