Рис. III.9
Изгиб.
Изгиб является наиболее сложным видом нагружения. Изгиб – деформация балки под действием моментов в вертикальной продольной или горизонтальной плоскостях (Рис. III.4).
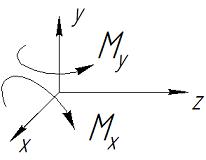
Рис. III. 4
Рассмотрим изгиб консольно заделанной балки (Рис. III.5).
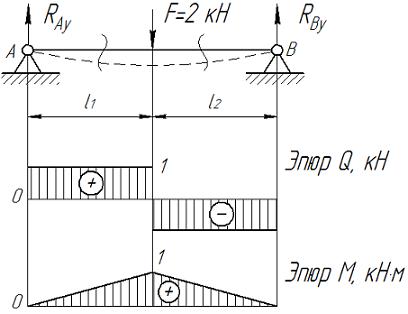
Рис. III.5
Изгибающий момент создается под действием концентрированной силы F. На балку действуют шарнирные опоры А и В, в связи с чем возникают реакции связей – RАy и RВy (Рис. III.6).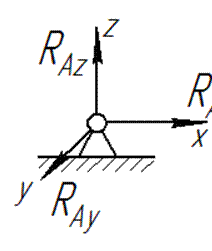
Расчет балки на прочность сводится к построению эпюров внутренних силовых факторов – поперечной силы Q и изгибающего внутреннего момента Мх. Решение задачи начинается с определения всех реакций связей. Очевидно, что:
 .
.
Используя метод сечений, мысленно рассечем балку сечениями и, откинув более нагруженную часть грузового участка (l1 или l2), рассмотрим I и II участки.
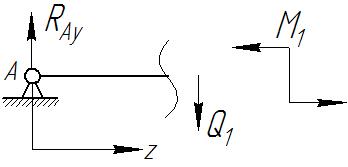
Рис. III. 7
Рассмотрим участок I (Рис. III.7). Равновесие участка обеспечивается, если воздействию внешней реактивной силы RAy будет противостоять внутренняя сила Q1. Образованная пара сил создает момент, который должен быть скомпенсирован изгибающим моментом Mx1.
Тогда:
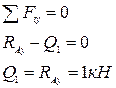
Условием неопрокидывания (неповорачивания) является нулевая сумма моментов внешних и внутренних сил относительно точки сечения:
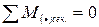 ,
,
тогда:
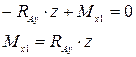
Если z =0, то Мх1 =0, если z = l 1, то Мх1 = RAy · l 1. Пусть l 1=1 м, тогда Мх1 = RAy · l 1=1·1=1 кН·м. Внутренний момент Мх1 не является постоянным на участке, в связи с увеличением z, и его проекция на эпюре – наклонная линия.
Аналогичные рассуждения проводятся для участка II (Рис. III.8) и для любых балок с любым видом нагружения.
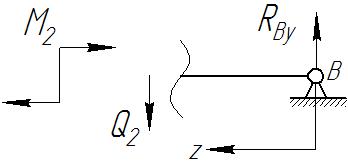
Рис. III.8
Правила знаков.
Внутреннее поперечное усилие Q положительно, если справа от сечения вектор Q направлен вниз, а слева от сечения – вверх, в противном случае Q принимает отрицательное значение (Рис. III.9, а).
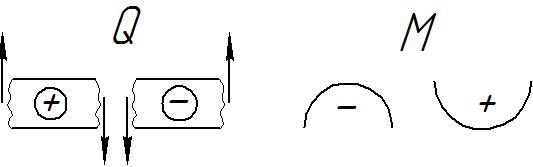
а) б)
Если внутренний изгибающий момент М изгибает балку вниз, то на эпюре его проекция положительна, если вверх – отрицательна (Рис. III.9, б).
Замечание. Данное правило определения знака М применимо только при построении эпюра, при составлении уравнений равновесия используется зависимость знака М от направления вращения момента.
Рассмотрим случай нагружения балки распределенной силой q (Рис. III.10).
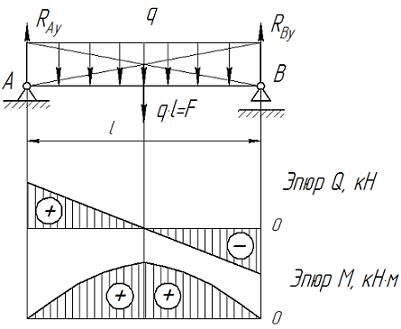
Рис. III.10
Очевидно, что:
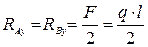 .
.
Рассмотрим участок слева от сечения (Рис. III.11).
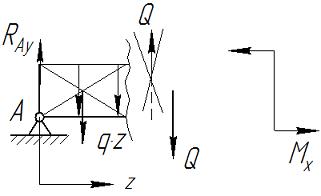
Рис. III. 11
Условием вертикального равновесия является уравнение:

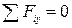
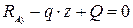 ,
,
откуда:
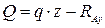
если z =0, то Q =- RAy, из чего следует то, что направление вектора Q выбрано неправильно. При увеличении z величина Q изменяется, проекция Q является наклонной линией.
Условие неопрокидывания:

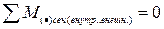
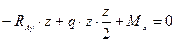 ,
,
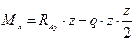 ,
,
если z =0, то Мх =0.
Из рис. III.10 видно, что балка максимально изогнется в середине балки и, следовательно, опасное сечение – середина балки, тогда как в точках А и В деформации минимальны, тогда:
если z =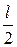 , то Мх =max
, то Мх =max
если z =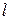 , то Мх =min.
, то Мх =min.
Правила проверки коррекции построения эпюр.
1. В местах приложения концентрированных внешних силовых факторов на соответствующих эпюрах наблюдаются переходы, равные величине внешних факторов.
2. При наличии концентрированных внешних сил эпюр поперечного усилия Q – горизонталь, а изгибающего момента М – наклонная линия.
3. Если внешняя нагрузка распределена по длине балки, то проекция Q на эпюре – наклонная линия, изгибающего момента М – парабола, причем выпуклость параболы – против направления распределенного усилия.
4. Поскольку
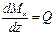 ,
,
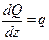 ,
,
то знак производной от Мх соответствует знаку поперечного усилия Q.
Рассмотрим случай осевого (центрального) нагружения (Рис.IV.1), в результате чего появляется внутреннее осевое усилие, приводящее к деформации (в данном случае – растяжение). Если на поверхность тела (стержня) нанести сетку линий, параллельных и перпендикулярных оси тела, то при нагружении расстояние между ними изменится, причем сами линии останутся взаимно перпендикулярными.
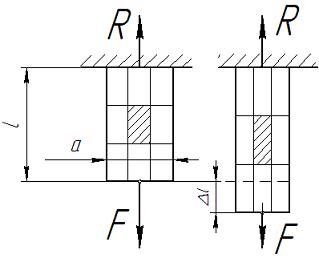
Рис. IV. 1
Рассмотрим деформацию выделенного элементарного участка (заштриховано). В результате нагружения участок удлиняется и сжимается, деформации балки можно описать относительными величинами – относительная продольная деформация ε и поперечная относительная деформация ε ΄:
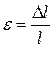 (IV.1)
(IV.1)
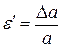 . (IV.2)
. (IV.2)
Величина, позволяющая сопоставить поперечные и продольные деформации, - коэффициент Пуассона μ:
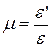 .
.
Упругость – свойство материала возвращаться к первоначальным размерам после снятия нагрузки. Однако абсолютно упругие тела встречаются очень редко, у высокопрочных материалов ε снижается лишь до 7-10%.
Используя отношение:
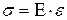 , (IV.3)
, (IV.3)
где Е – модуль продольной упругости (модуль Юнга I рода), характеризующий упругость материала и являющийся основной компонентой прочности материала, выведем зависимость, позволяющую определить деформации тела.
Используя формулы (IV.1), (IV.3), а также:
 , (IV.4)
, (IV.4)
где σ – нормальное напряжение поперечного сечения стержня, Н/м2;
N – равнодействующая внутренних сил, действующих в сечении, Н;
А – площадь сечения, м2,
получим:
 ,
,
тогда:
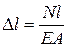 , (IV.5)
, (IV.5)
где ЕА – жесткость нагруженного усилиями материала, по своему физическому смыслу представляющая собой удельную энергию – количество энергии, затраченной на единичное удлинение единичного сечения.
Зависимость, описываемая формулой (IV.5), носит название закона Гука.
Закон Гука позволяет описать «поведение» материала, а также оценить механические характеристики конструкционных материалов. Механические характеристики материала определяются опытным (экспериментальным) путем. В соответствии с целевыми значениями методы определения физико-механических характеристик материала делятся на статический метод, в процессе которого образец материала подвергается не изменяющейся во времени нагрузкой, и динамический метод, в ходе которого используются величины, меняющиеся во времени.
Простейший эксперимент, позволяющий определить основные механические характеристики материала – нагружение образца продольными усилиями. Опыт проводится с последующим построением диаграммы (или растяжения) (Рис. IV.2). 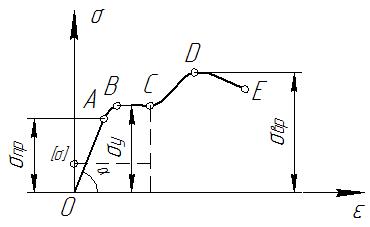
Рис. IV. 2
Как видно, вначале, в зоне ОА, деформации растут пропорционально напряжениям до некоторого предельного напряжения σпр – это зона упругих деформаций, или зона пропорциональности. В зоне АВ материал еще сохраняет упругие свойства, но прямая зависимость между деформациями и напряжениями нарушается, в связи с чем зона называется зоной непропорциональности. Для зоны ВС – зоны текучести – характерно то, что небольшое увеличение нагрузки приводит к большим деформациям. Участок СD – зона местной текучести, зона образования шейки. Зона DE соответствует разрушающей нагрузке – зона временной упругости.
Пластичный материал допускает значительные деформации без видимых признаков разрушения, хрупкий – разрушается при относительно небольших деформациях. Разрыв образца хрупкого материала наступает внезапно при очень малых деформациях и без образования шейки. График диаграммы растяжения для такого материала дан на рис. IV.3.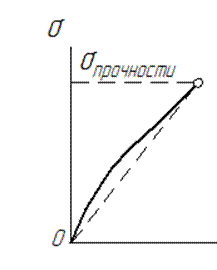 Обработка описанной диаграммы сводится к тому, что наклонная линия аппроксимируется с прямой (штриховая), задается угол между этой прямой и осью 0ε и оценивается модуль упругости I рода Е (для хрупких материалов Е составляет 1,1…1,6·105 МПа, тогда как Е пластичных материалов достигает 2·105 МПа).
Обработка описанной диаграммы сводится к тому, что наклонная линия аппроксимируется с прямой (штриховая), задается угол между этой прямой и осью 0ε и оценивается модуль упругости I рода Е (для хрупких материалов Е составляет 1,1…1,6·105 МПа, тогда как Е пластичных материалов достигает 2·105 МПа).
Диаграмма напряжения позволяет определить некоторые характеристики материала, а именно:
- модуль упругости I рода Е, равный тангенсу угла наклона прямой 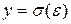 в зоне пропорциональности диаграммы растяжения;
в зоне пропорциональности диаграммы растяжения;
- рабочая зона материала, определяемая пределом текучести σт, который, в свою очередь, связан с предельным нормальным напряжением [ σ ] данного материала:
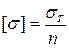 ,
,
где n – коэффициент запаса прочности, равный для пластичных материалов n =1,2…1,5, для хрупких материалов n =2…5.
Результаты настоящего метода можно распространить и на другие виды нагружения. Например, при скручивании материала основной его физико-механической характеристикой будет предельное касательное напряжение [ τ ], равное:
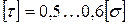 .
.
 2014-02-09
2014-02-09 1372
1372
