Тема 2 Комплексные числа

Свойства изоморфных колец

1. ~, ~~.

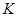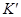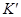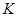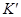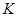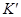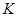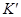2. ~, – ноль кольца , – ноль кольца , – отображение, осуществляющее изоморфизм колец и , то .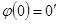

3. , .

4. Если в 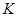существует , то в 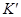существует единица и , .

Следствие: Кольцо, изоморфное полю, является полем.

Рассмотрим декартово произведение , где – множество действительных чисел. .

Введем операции над парами действительных чисел:

Пусть , .

Тогда , .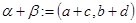

Определение 2.1: Множество с введенными выше операциями сложения и умножения элементов называется множеством комплексных чисел и обозначается .

Определение 2.2: .

Теорема 2.1: Множество является полем.

Следствие 1: , .

Следствие 2: , где , , , .

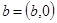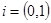Комплексные числа вида отождествляют с действительными числами, то есть .

Определение 2.3: Комплексное число 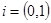называется мнимой единицей и .