Пусть дана прямоугольная таблица размером 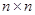 , которая называется матрицей.
, которая называется матрицей.
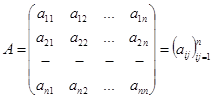
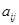 – элемент матрицы, расположенный в
– элемент матрицы, расположенный в 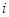 -й строке и
-й строке и 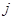 -м столбце.
-м столбце.
Определение 3.7: Определителем матрицы  называется алгебраическая сумма
называется алгебраическая сумма 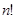 слагаемых, составленная следующим образом: слагаемыми являются всевозможные произведения из
слагаемых, составленная следующим образом: слагаемыми являются всевозможные произведения из  элементов матрицы
элементов матрицы  , взятых по одному из каждой строки и из каждого столбца матрицы, причем слагаемое берется со знаком плюс, если его индексы составляют четную подстановку, и со знаком минус – в противном случае.
, взятых по одному из каждой строки и из каждого столбца матрицы, причем слагаемое берется со знаком плюс, если его индексы составляют четную подстановку, и со знаком минус – в противном случае.
Подстановка получается следующим образом: всякое слагаемое определителя имеет вид: 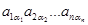 и определяет подстановку
и определяет подстановку 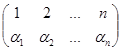 , о четности которой и говорится в определении.
, о четности которой и говорится в определении.
Определитель матрицы  обозначается одним из следующих способов:
обозначается одним из следующих способов: 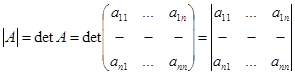 .
.
В частности: 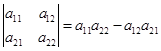 ,
,
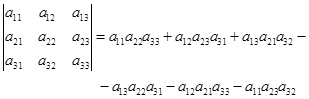
Определение 3.8: Матрица 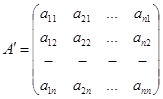 называется транспонированной матрицей по отношению к матрице
называется транспонированной матрицей по отношению к матрице  .
.
У матрицы 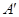 столбцами являются строки матрицы
столбцами являются строки матрицы  , а строками – столбцы матрицы
, а строками – столбцы матрицы  .
.
Если 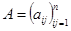 , то
, то 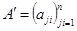 .
.
 2014-02-13
2014-02-13 1104
1104








