Определение 3.10: Пусть дан определитель матрицы 
 -го порядка. Выделим в нем
-го порядка. Выделим в нем 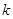 строк (
строк (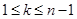 ) и
) и 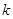 столбцов. Элементы матрицы
столбцов. Элементы матрицы  , расположенные на пересечении выделенных строк и столбцов, образуют определитель
, расположенные на пересечении выделенных строк и столбцов, образуют определитель 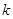 -го порядка, который называется минором данного определителя и обозначается
-го порядка, который называется минором данного определителя и обозначается 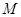 .
.
Замечание: Элементы матрицы являются минором 1-го порядка.
Обозначим номера выделенных строк через 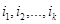 , а столбцов –
, а столбцов – 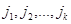 .
.
Определение 3.11: После вычеркивания выделенных 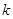 строк и
строк и 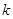 столбцов из матрицы
столбцов из матрицы  остается определитель порядка
остается определитель порядка 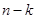 , который называется дополнительным минором
, который называется дополнительным минором 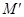 к минору
к минору 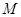 .
.
Определение 3.12: Обозначим 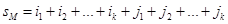
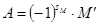 называется алгебраическим дополнением к минору
называется алгебраическим дополнением к минору 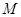 .
.
В частности, обозначим через 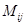 дополнительный минор к минору
дополнительный минор к минору 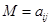 , а алгебраическое дополнение –
, а алгебраическое дополнение – 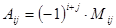 .
.
Теорема 3.5: Произведение любого минора на его алгебраическое дополнение в определителе 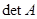 является алгебраической суммой, слагаемые которой будут слагаемыми данного определителя, причем они взяты с теми же знаками, с которыми они входят в
является алгебраической суммой, слагаемые которой будут слагаемыми данного определителя, причем они взяты с теми же знаками, с которыми они входят в 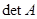 .
.
 2014-02-13
2014-02-13 631
631








