Тема 2. Минимизация дизъюнктивных нормальных форм

Лекция 1. Основные понятия теории минимизации дизъюнктивных нормальных форм

1) Введение в проблему минимизации дизъюнктивных нормальных форм (ДНФ) [1,2,3,5]

Допустимой конъюнкцией или импликантом функции 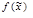называется элементарная конъюнкция К над множеством переменных 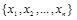, такая, что 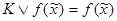. Импликант К функции 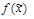называется простым импликантом, если после отбрасывания любой буквы из К получается э.к., не являющаяся импликантом функции .

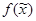Дизъюнкция всех простых импликантов функции 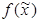называется сокращенной д.н.ф. функции 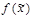. Д.н.ф. называется: минимальной, если она имеет наименьшее число букв среди эквивалентных ей д.н.ф.; кратчайшей, если она имеет наименьшую длину среди эквивалентных ей д.н.ф.; тупиковой, если отбрасывание любого слагаемого или буквы приводит к неэквивалентной д.н.ф. Если э.к. K является импликантом функции 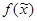, то множество 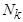=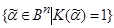образует грань, содержащуюся в множестве 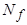=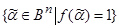. Эта грань является интервалом функции 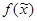, соответствующим импликанту K. Интервал функции 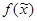, не содержащийся ни в каком другом интервале, называется максимальным интервалом. Максимальные интервалы соответствуют простым импликантам функции .

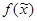Метод Блейка получения сокращенной д.н.ф. из произвольной д.н.ф. состоит в применении правил обобщенного склеивания 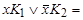= 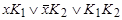и поглощения 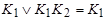. Правила применяются слева направо. Сперва производятся операции обобщенного склеивания, пока это возможно, на втором — операции поглощения. Для построения сокращенной д.н.ф. можно использовать геометрический или табличный методы (с помощью минимизирующей карты).

2) Понятие об индексе (коэффициенте) простоты [1,2,3,5]

3) Сокращенная, тупиковые и кратчайшие дизъюнктивные нормальные формы [1,2,3,5]

Литература:

1. Яблонский С.В. Введение в дискретную математику. М.:Высш. шк., 2001. – 384 с.

2. Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. М.: Наука, 1977. – 386 с.

3. Гиндикин С. Г. Алгебра логики в задачах. М.: Наука, 1972.- 288 с.

4. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.

5. Донской В. И. Дискретная математика. – Симферополь: Сонат, 2000. –356 с.