Лекция 1. Теория кодирования. Общие положения
1) Общие положения теории кодирования [1,2,3]
Пусть 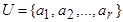 — алфавит. Конечная последовательность символов из U называется словом в алфавите U. Через S(U) обозначим множество всех слов в алфавите U.
— алфавит. Конечная последовательность символов из U называется словом в алфавите U. Через S(U) обозначим множество всех слов в алфавите U.
Пусть U и B — два алфавита. Однозначное отображение F произвольного подмножества 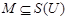 на подмножества
на подмножества  называется кодированием. При этом слова из M называются сообщениями, а их образы — кодами сообщений. Множество С называется кодом множества сообщений М. Алфавит U называется алфавитом сообщений, а алфавит В — кодирующим алфавитом. Кодирование F называется взаимно однозначным, если каждый код сообщения является кодом ровно одного сообщения.
называется кодированием. При этом слова из M называются сообщениями, а их образы — кодами сообщений. Множество С называется кодом множества сообщений М. Алфавит U называется алфавитом сообщений, а алфавит В — кодирующим алфавитом. Кодирование F называется взаимно однозначным, если каждый код сообщения является кодом ровно одного сообщения.
Пусть задано отображение 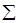 букв алфавита U в множество S (B) вида
букв алфавита U в множество S (B) вида
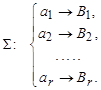
Кодирование 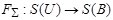 , удовлетворяющее свойствам:
, удовлетворяющее свойствам:
1) 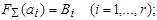
2) 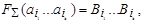
где под произведением слов АВ понимается приписывание слова В справа к слову А, называется алфавитным кодированием, задаваемым схемой 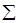 .
.
2) Свойство префикса. Критерий однозначности декодирования [1,2,3]
Если 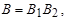 то
то 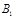 называется префиксом, а
называется префиксом, а 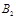 — суффиксом слова В. Префикс (суффикс) слова В называется собственным, если он отличен от пустого слова (обозначаемого через
— суффиксом слова В. Префикс (суффикс) слова В называется собственным, если он отличен от пустого слова (обозначаемого через 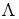 ) и от самого слова В. Длиной слова называется число букв в нем. Схема
) и от самого слова В. Длиной слова называется число букв в нем. Схема 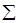 обладает свойством префикса, если для любых слов
обладает свойством префикса, если для любых слов 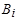 и
и 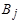 (
(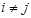 ) из С(
) из С(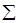 ) слово
) слово 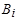 не является префиксом слова
не является префиксом слова 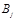 .
.
Теорема. Алфавитный код С(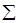 ) является однозначно декодируемым тогда и только тогда, когда в графе
) является однозначно декодируемым тогда и только тогда, когда в графе 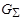 отсутствуют контуры и петли, проходящие через вершину
отсутствуют контуры и петли, проходящие через вершину 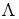 .
.
Лекция 2. Коды, исправляющие ошиибки
1) Коды Хэмминга [1,2,3]
2) Метрические свойства кодов [1,2,3]
Литература:
1. Яблонский С.В. Введение в дискретную математику. М.:Высш. шк., 2001. – 384 с.
2. Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. М.: Наука, 1977. – 386 с.
3. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.
 2014-02-13
2014-02-13 949
949








