Тема 6. Конечные автоматы

Лекция 1. Детерминированные функции

1) Функции, преобразующие последовательности [1,2,3,4]

Пусть А — непустой конечный алфавит. Элементы алфавита называются буквами или символами. Последовательность символов из алфавита А называется словом. Количество символов в слове называется длиной слова. Множество всех слов 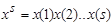длины s в алфавите А обозначим через 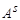. Пустое слово (длины 0) обозначается 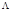, бесконечное слово — 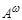, т.е. множество всех символов 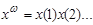, где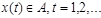

Слово w, полученное приписыванием справа слова w ₂ к слову w ₁, называется соединением слов. Слова w ₁ и w ₂ называются префиксом и суффиксом слова w соответственно.

Пусть А и В — конечные непустые алфавиты. Отображение: 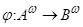называется детерминированной функцией (оператором), если:

а) для всякого s >0 s -й символ y (s) слова 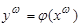является однозначной функцией первых s символов x (1),..., x (s) слова ;

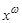б) если у слов 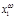и 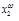префиксы длины s совпадают, то совпадают также префиксы у слов 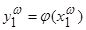и .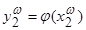

Удобно считать, что детерминированная функция 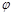реализуется некоторым дискретным устройством (автоматом), работающим в дискретные моменты времени t =1,2,..., когда на вход автомата подается сигнал x (t), а на выходе появляется сигнал y (t). Слова 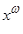называются входными, 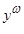— выходными.

2) Деревья, задающие детерминированные функции [1,2,3,4]

Графическим изображением детерминированной функций является информативное дерево. Количество классов эквивалентных поддеревьев в информативном дереве называется весом детерминированной функции.

Литература:

1. Яблонский С.В. Введение в дискретную математику. М.:Высш. шк., 2001. – 384 с.

2. Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. М.: Наука, 1977. – 386 с.

3. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.

4. Донской В. И. Дискретная математика. – Симферополь: Сонат, 2000. –356 с.

Лекция 2. Ограниченно-детерминированные функции

1) Ограниченно-детерминированные функции [1,2,3,4]

Детерминированная функция называется ограниченно - детерминированной функцией (о.д.ф.), если она имеет конечный вес.

2) Диаграмма Мура [1,2,3,4]

О.д.ф. может быть представлена диаграммой Мура, каноническими уравнениями, таблицами и схемами.

Процесс вычисления на основании диаграмм Мура может быть

истолкован следующим образом:

в момент времени t -1 вычислительный процесс находился в состоянии

q (t -1), при наступлении момента времени t, мы переместимся по дуге x (t) в состояние q (t) на диаграмме Мура и получим выходное значение y (t). Следовательно, пара значений (q (t -1), x (t)) определяет пару значений (q (t), y (t)), где

x (t) — значение аргумента на шаге t,

y (t) — значение функции,

q (t) — номер класса эквивалентности.

3) Каноническая таблица и канонические уравнения [1,2,3,4]

Утверждение. Любую о.-д. функцию можно представить в виде системы канонических уравнений

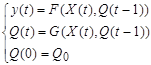, t=1,2,…,

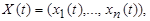
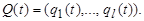
Элементом единичной задержки называется ограниченно-детерминированный оператор 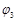, задаваемый системой:

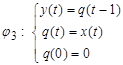
Литература:

1. Яблонский С.В. Введение в дискретную математику. М.:Высш. шк., 2001. – 384 с.

2. Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. М.: Наука, 1977. – 386 с.

3. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.