Лекция 1. Тьюринговские модели

Тема 1: Модели вычислений

1) Модификации тьюринговских моделей [1,2,3,4,5,6,7,8,9]

Понятие алгоритма - одно из центральных в математике и, по крайней мере, не менее важное, чем понятие функции. Функция – это соответствие между двумя множествами X и Y, согласно которому для каждого элемента 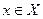указывается единственный элемент у=f (x). В ряде случаев оказывается важным не только задать функцию (соответствие) f, но и указать способ нахождения значения f (x)для всякого заданного .

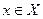Например, функция Лапласа:

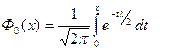(1.1)

полностью определена выражением (1.1) для любого 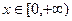, однако способ вычисления по заданному х значения 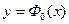этим выражением не определен.

Алгоритм принципиально отличается от функции тем, что устанавливая соответствие 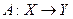, он определяет не только единственный элемент у =А (х) для всякого 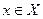, но и способ поиска этого элемента при помощи конечной последовательности достаточно простых (очевидных, элементарных) действий, которые называют шагами.

Главный элемент, необходимый для строгого определения алгоритма - это набор (множество) элементарных действий, из которых строятся конечные последовательности шагов. Математики, занимавшиеся формализацией понятия алгоритма, предложили pяд способов выбора множества элементарных действий и, соответственно, формальных моделей, уточняющих интуитивное понятие алгоритма.

Наиболее удачные формализации понятия алгоритма были разработаны А.А. Марковым (элементарные действия - подстановки), А. Тьюрингом (элементарные действия - команды абстрактной математической машины), Э.Постом, М.Минским.

Впоследствии оказалось, что разработанные этими математиками модели алгоритмов эквивалентны в том смысле, что классы решаемых с их помощью задач совпадают. В связи с этим А. Черч сформулировал гипотезу, известную как Тезис Черча, обобщенный смысл которой состоит в том, что класс задач, решаемых в любой из построенных математиками эквивалентных формальных моделей алгоритмов, и есть класс всех задач, которые могут быть решены “интуитивно алгоритмическими” методами.

Для математиков-программистов несложно переписать алгоритм решения задачи, подготовленный на одном языке программирования, на другой язык. Если такая трансляция, скажем, с языка PASCAL на язык С++ является делом достаточно простым, то трансляция тьюринговского алгоритма в марковский может оказаться значительно сложнее. Но есть одно обстоятельство, которое существенно снижает значение того, в какой формальной или прикладной системе (ЭВМ, язык) записан алгоритм.

Пусть в модели (машине) 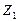произвольный алгоритм А выполняется за 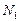шагов; каждый элементарный шаг в модели 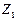может быть представлен эквивалентной последовательностью не более чем из 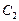шагов в модели 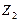. Тогда, заменяя все элементарные действия системы 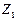, реализующие алгоритм А, на эквивалентные последовательности элементарных действий системы 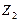, получим эквивалентный А алгоритм в 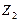выполняющийся не более чем за 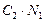шагов.

Коэффициент 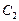является константой и параметром конкретной алгоритмической модели (машины). Это наводит на мысль о целесообразности оценивания сложности вычислений с точностью до константы. Для математиков с точки зрения теории вычислимости безразлично, какая именно алгоритмическая модель выбрана для построения или анализа алгоритма. Выбор алгоритмической модели, как правило, определяется удобством доказательства свойств алгоритмов, их сравнения, получения теоретических результатов и конкретных прикладных реализаций.

2) Сложность тьюринговских вычислений [1,2,3,4,5,6,7,8,9]

Математики, занимающиеся исследованиями в области теории алгоритмов, чаще всего используют частично-рекурсивные функции и машину Тьюринга, хотя не исключаются и другие алгоритмические модели и языки, вплоть до некоторым образом «расширенных» языков программирования высокого уровня.

Используя языки высокого уровня, математик легче воспринимает логику алгоритма, быстрее оценивает его сложность, если только отдельные блоки алгоритма, представленные на используемом языке, имеют очевидную или легко оцениваемую сложность.

Используя машину Тьюринга, несложно оценивать не только число шагов выполнения алгоритма как показатель «временн о й» сложности, но и число использованных ячеек тьюринговской ленты как показатель «объемной» сложности или требуемого объема памяти. Поэтому в теории сложности часто используется алгоритмическая модель Тьюринга.

В терминах машины Тьюринга (МТ) как алгоритмической модели можно сформулировать следующие важные определения.

Пусть 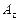- тьюринговский алгоритм решения некоторой задачи z из класса Z. Начальная информация (исходные данные) записана на ленте МТ и занимает некоторое количество n ячеек. Это число ячеек называется размером (входа) задачи. Число шагов МТ, выполняемых алгоритмом 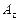при решении задачи z, называется временной сложностью алгоритма 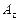. Обычно временную сложность представляют как функцию размера задачи: 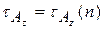. В процессе выполнения алгоритма изменяется запись на ленте МТ, и головка машины совершает перемещение в пределах участка ленты oт некоторой ячейки 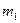до ячейки 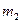. Этот участок ленты называют рабочей зоной, а длину рабочей зоны 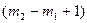- пространственной сложностью 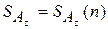алгоритма 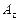. Естественно принимать за размер входа число символов, используемых для записи начальной информации. При этом нужно отметить, что разные способы кодирования, вообще говоря, изменяют размер входа.

Литература:

1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. – 416 с.

2. Ахо А., Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. – 536 с.

3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.

4. Донской В. И. Дискретная математика. –Симферополь: Сонат, 2000. –356 с.

5. Липский В. Комбинаторика для программистов. М.: Мир, 1988. – 215 с.

6. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физико-математическая литература, 1995. – 256 с

7. Линдон Р. Заметки по логике. М.: Мир, 1968. – 128 с.

8. Оре О. Теория графов. М.: Наука, 1980. – 336 с.

9. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.