Теорема_5.1. (Сoоk S.A., 1971). Задача выполнимости КНФ является NР- полной.
Доказательство. Достаточно убедиться, что:
а) 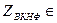 NР и
NР и
б) что любая задача из NР полиномиально сводится к  .
.
Покажем выполнение условия а). Недетерминированный алгоритм, решающий задачу  при длине КНФ, равной m, и числе переменных n, состоит в следующем.
при длине КНФ, равной m, и числе переменных n, состоит в следующем.
1о Недетерминированным оператором выбрать 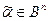 ;
;
2о Просмотреть в каждой из m скобок не более, чем n значений 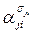 литералов
литералов 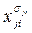 и дать ответ «выполнима», если в каждой скобке найдется хотя бы один литерал, принимающий значение 1, иначе дать ответ «не выполнима».
и дать ответ «выполнима», если в каждой скобке найдется хотя бы один литерал, принимающий значение 1, иначе дать ответ «не выполнима».
Очевидно, для этого недетерминированного алгоритма сложность может быть оценена как o(mn) и является полиномиальной, поэтому 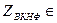 NP.
NP.
Теперь покажем выполнение условия б). Убедимся, что любая задача из NP полиномиально сводима к  .
.
Сначала отметим, что любая задача вычисления свойств может быть представлена следующим образом: по заданному объекту х выяснить, существует ли объект у такой, что R(x,y)=1. В проблеме  объект х - формула, а у - набор значений переменных. Свойство R(x,y) состоит в том, что на наборе у формула х выполнима. Любая задача из NP может быть сформулирована как задача вычисления свойства. Суть дальнейшего доказательства состоит в указании процедуры, которая для любого полиномиального недетерминированного алгоритма вычисления свойства (выходом которого являются ответы «истина» или «ложь») и для любой допустимой начальной информации такого алгоритма строит логическое выражение в виде КНФ, и это выражение является выполнимым тогда и только тогда, когда алгоритм определяет ответ «да», причем построение этого логического выражения из формального описания недетерминированного алгоритма и его входной информации можно выполнить за полиномиальное число шагов. Иначе говоря, будет доказана полиномиальная сводимость любой задачи из NP к задаче проверки выполнимости некоторой конъюнктивной нормальной формы.
объект х - формула, а у - набор значений переменных. Свойство R(x,y) состоит в том, что на наборе у формула х выполнима. Любая задача из NP может быть сформулирована как задача вычисления свойства. Суть дальнейшего доказательства состоит в указании процедуры, которая для любого полиномиального недетерминированного алгоритма вычисления свойства (выходом которого являются ответы «истина» или «ложь») и для любой допустимой начальной информации такого алгоритма строит логическое выражение в виде КНФ, и это выражение является выполнимым тогда и только тогда, когда алгоритм определяет ответ «да», причем построение этого логического выражения из формального описания недетерминированного алгоритма и его входной информации можно выполнить за полиномиальное число шагов. Иначе говоря, будет доказана полиномиальная сводимость любой задачи из NP к задаче проверки выполнимости некоторой конъюнктивной нормальной формы.
Построение процедуры сводимости выполняется в терминах алгоритмической системы Тьюринга.
Итак, произвольная задача z вычисления свойства R(x,y) из класса NР может быть выполнена на недетерминированной машине Тьюринга НДМТ с полиномиальной проверкой, т.е. за число шагов, ограниченное полиномом от размера задачи l(х)+l(y) = n. Полиномиальной при этом будет и длина рабочей зоны ленты НДМТ Т = Р(n), где P(.) - некоторый полином (предположение о том, что длина рабочей зоны на ленте для задачи z не ограничена полиномом, противоречило бы принадлежности z классу NР. Ячейки НДМТ обозначим целочисленными номерами.... -2, -1, 0,+1,+2,.... Расположение начальной информации на ленте представлено на рис. 5.1. в ячейках с номерами 1,……, n.
 Произвольное начало отсчета
Произвольное начало отсчета
| … | -2 | -1 | … | n | … |





Рис. 5.1 Расположение информации на ленте
Вычисления при любом допустимом значении объекта у происходят в зоне ленты [- Т, Т ] и завершаются не более чем за Т шагов (тактов работы НДМТ). Машина, начав работу в конфигурации 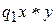 , останавливается в конфигурации
, останавливается в конфигурации 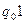 , если свойство R(x, y) выполнено, и в
, если свойство R(x, y) выполнено, и в 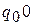 - в противнем случае. Здесь
- в противнем случае. Здесь 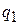 - начальное, а
- начальное, а 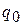 - заключительное состояние НДМТ. Построим КНФ Ф такую, что любая задача проверки (распознания) свойства (в общем виде:
- заключительное состояние НДМТ. Построим КНФ Ф такую, что любая задача проверки (распознания) свойства (в общем виде: 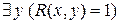 ) полиномиально сводится к проверке выполнимости КНФ
) полиномиально сводится к проверке выполнимости КНФ
Ф = В & C & D & Е & F & G,
где В, С, D, E, F, G - дизъюнкты, имеющие следующий смысл:
В = 1 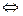 На каждом шаге головка машины обозревает ровно одну ячейку ленты.
На каждом шаге головка машины обозревает ровно одну ячейку ленты.
С = 1 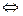 В каждой ячейке на каждом шаге записан в точности один символ.
В каждой ячейке на каждом шаге записан в точности один символ.
D = 1 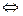 На каждом шаге работы машина находится ровно в одном состоянии.
На каждом шаге работы машина находится ровно в одном состоянии.
Е = 1 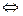 Начальная конфигурация машины имеет вид
Начальная конфигурация машины имеет вид 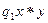 .
.
F = 1 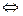 Машина работает по тьюринговской программе.
Машина работает по тьюринговской программе.
G = 1 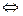 Заключительная конфигурация машины имеет вид
Заключительная конфигурация машины имеет вид 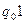 , если Р(х,у) = 1.
, если Р(х,у) = 1.
Обозначим 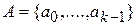 ,
,  - внешний и внутренний алфавиты НМДТ; t – произвольный шаг выполнения алгоритма,
- внешний и внутренний алфавиты НМДТ; t – произвольный шаг выполнения алгоритма, 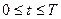 ; s – текущий номер ячейки,
; s – текущий номер ячейки, 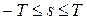 ; i и j - текущие номера символов алфавитов А и Q,
; i и j - текущие номера символов алфавитов А и Q, 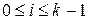 ,
, 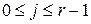 .
.
Введем по определению следующие логические переменные:
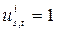 , если на шаге t, обозревая ячейку s, машина воспринимает символ с номером i, иначе эта переменная равна нулю.
, если на шаге t, обозревая ячейку s, машина воспринимает символ с номером i, иначе эта переменная равна нулю.
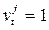 , если на шаге t машина находится в состоянии с номером j, иначе эта переменная равна нулю.
, если на шаге t машина находится в состоянии с номером j, иначе эта переменная равна нулю.
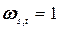 , если на шаге t головка машины обозревает ячейку с номером s, иначе эта переменная равна нулю.
, если на шаге t головка машины обозревает ячейку с номером s, иначе эта переменная равна нулю.
Используя введенные логические переменные, можно записать в виде формул следующие логические условия.
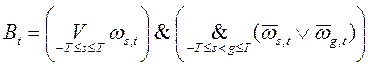 ;
;
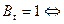 на шаге t машина обозревает хотя бы одну ячейку и при этом никакие две ячейки одновременно, т. к.
на шаге t машина обозревает хотя бы одну ячейку и при этом никакие две ячейки одновременно, т. к. 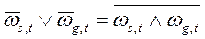 . Тогда
. Тогда
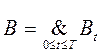 .
.
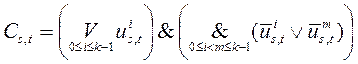 ;
;
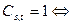 на шаге t в ячейке s записан ровно один символ. Тогда
на шаге t в ячейке s записан ровно один символ. Тогда
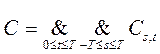 .
.
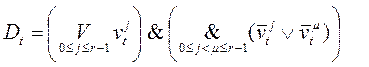 ;
;
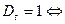 на шаге t машина находится ровно в одном состоянии. Тогда
на шаге t машина находится ровно в одном состоянии. Тогда
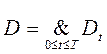 .
.
В начальном положении (t= 0 ) головка машины обозревает ячейку с номером 1 в состоянии q1, а в первых n - ячейках записаны символы слова Х = х (1)... х (n), за ним - разделительный знак «*», после чего - слово Y= y (1)... y (q) и далее - пустые ячейки. Выполнение такой начальной конфигурации равносильно Е = 1, где 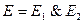
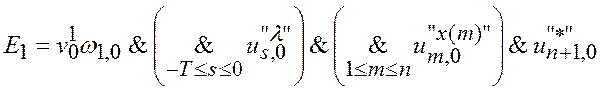 ;
;
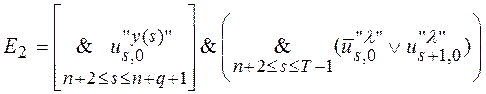 ,
,
где l - пустой символ, а запись 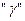 означает индекс символа
означает индекс символа 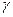 в ленточном алфавите.
в ленточном алфавите.
Полиномиальная программа проверки свойства состоит из тьюринговских команд:
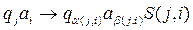 .
.
Здесь 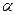 - функция смены состояний НМТ,
- функция смены состояний НМТ, 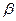 - функция, определяющая записываемый на ленту символ,
- функция, определяющая записываемый на ленту символ, 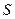 - функция, определяющая движение головки машины,
- функция, определяющая движение головки машины, 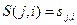 . Введем вспомогательную функцию –
. Введем вспомогательную функцию –
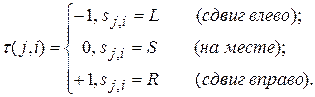
Пусть по определению 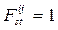 , если на шаге t, находясь в состояний
, если на шаге t, находясь в состояний 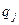 , машина обозревает ячейку с номером s, в которой записан символ
, машина обозревает ячейку с номером s, в которой записан символ 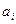 , и смена состояния и записи в ячейке осуществляется в соответствии с программой, причем при отсутствии головки над ячейкой s запись в этой ячейке не изменяется; в противном случае
, и смена состояния и записи в ячейке осуществляется в соответствии с программой, причем при отсутствии головки над ячейкой s запись в этой ячейке не изменяется; в противном случае 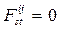 .
.
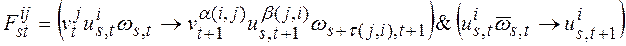 .
.
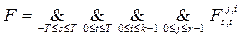 .
.
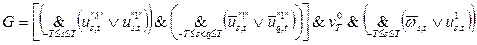 ,
,
где выражение в квадратных скобках соответствует тому, что на последнем шаге Т на ленте записаны символы l(пусто) и 1, причем единица содержится не более чем в одной ячейке; сомножитель 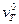 соответствует нахождению машины на шаге Т в состоянии
соответствует нахождению машины на шаге Т в состоянии  ; последняя конъюнкция обеспечивает условие наличия в обозреваемой ячейке символа 1.
; последняя конъюнкция обеспечивает условие наличия в обозреваемой ячейке символа 1.
Приведенные выше выражения позволяют заключить, что формула Ф = В & C & D & Е & F & G будет являться КНФ, если привести промежуточные эквивалентные преобразования:
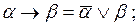
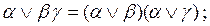
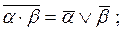
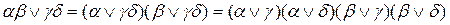 .
.
Условие Ф = 1 равносильно тому, что найдется такое допустимое значение у, при котором машина, начав работу в конфигурации 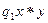 перейдёт в конфигурацию
перейдёт в конфигурацию 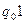 согласно тьюринговской программе полиномиальной проверки.
согласно тьюринговской программе полиномиальной проверки.
Если задача z имеет положительный ответ, то для некоторого допустимого у выполнено R(x,y)=1. В этом случае, назначив значения переменных 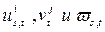 на основе работы машины над начальной конфигурацией
на основе работы машины над начальной конфигурацией 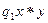 , получим набор, на котором Ф=1. Обратно, если существует набор, обращающий Ф в единицу, то значения переменных
, получим набор, на котором Ф=1. Обратно, если существует набор, обращающий Ф в единицу, то значения переменных 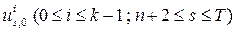 в этом наборе определяют слово у, такое, что машина переводит
в этом наборе определяют слово у, такое, что машина переводит 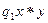 в
в 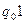 . Следовательно, задача z сведена к задаче выполнимости КНФ.
. Следовательно, задача z сведена к задаче выполнимости КНФ.
Очевидно, что длина записи формулы Ф при любом способе ее представления в виде слова над конечным алфавитом ограничена некоторым полиномом от размера входа задачи, и сведение задачи z к задаче  осуществимо за полиномиальное время.
осуществимо за полиномиальное время.
Теорема полностью доказана.
2) Класс NPC – универсальных переборных задач и приемы доказательства NP-полноты [1,2,3,4,5,6,7,8,9]
Пусть Г =(Х, U) - конечный граф, Х - множество вершин графа, U - множество ребер. Не теряя общности, можно обозначить вершины натуральными числами: Х = {1,2,..., n }, а ребра задать булевой матрицей 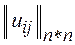 такой, что
такой, что 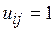 , если ребро (i,j) имеется в графе Г, и
, если ребро (i,j) имеется в графе Г, и 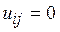 , если ребра (i,j) в графе Г нет. Граф называют полным, если любые его две вершины соединены ребром. Граф
, если ребра (i,j) в графе Г нет. Граф называют полным, если любые его две вершины соединены ребром. Граф 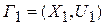 называют подграфом графа Г, если
называют подграфом графа Г, если 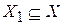 и
и 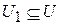 .
.
Задача о полном подграфе состоит в том, чтобы по заданному графу Г выяснить, существует ли в Г полный подграф с 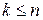 вершинами.
вершинами.
Теорема 7.1. Задача о полном подграфе является NP - полной.
Доказательство. Для удобства обозначим задачу о полном подграфе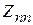 . Начальной информацией о задаче
. Начальной информацией о задаче 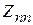 является число
является число 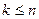 и матрица
и матрица 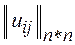 а) Докажем, что
а) Докажем, что 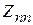 Î NP. Для этого выписываем N- программу:
Î NP. Для этого выписываем N- программу:
УСПЕХ:= TRUE; //Предположим, k-полный подграф существует
// Недетерминированный выбор k вершин
Set:= [1.. n ];
for i:= 1 to k dо
begin
node:= CHOOSE(Sеt);
v[i]:= node;
Set:=Set\(nodе)
еnd;
// Полиномиальная проверка
for i:= 1 tо k-1 do
for j:= i +1 tо k dо
if u(v[i],v[j])=0 then УСПЕХ:=FALSE;
write(УСПЕХ);
Очевидно, что сложность приведенной N-программы может быть оценена как О(n(n-1)/2), т.е. полиномиально, откуда следует, что 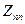 Î NP.
Î NP.
б) Докажем, что 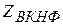 µ
µ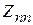 . Поскольку ранее мы убедились, что
. Поскольку ранее мы убедились, что 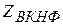 - NP-полная задача, то из полиномиальной сводимости
- NP-полная задача, то из полиномиальной сводимости  µ
µ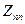 будет следовать полиномиальная сводимость любой задачи класса NP к
будет следовать полиномиальная сводимость любой задачи класса NP к 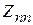 .
.
 2014-02-13
2014-02-13 503
503








