Лекция 1. Сравнительный анализ разных по сложности задач и их решения при повышении быстродействия компьютеров

Тема 4. Класс Р и неразрешимые полиномиальные задачи

1) Класс Р. Сравнительный анализ разных по сложности задач и их решения при повышении быстродействия компьютеров [1,2,3,4,5,6,7,8,9]

Временная (пространственная) сложность называется полиномиальной, если имеет вид P (n), где P (.) - некоторый полином от размера входа задачи n.

Определение 4.1. Классом Р называется множество всех задач, для которых существует алгоритм решения, имеющий полиномиальную сложность.

Алгоритмы с полиномиальной сложностью называют эффективными в отличие от алгоритмов, для которых временная или пространственная сложность как функции размера задачи не могут быть представлены полиномами. Алгоритмы, сложность которых оценивается как 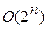(с экспоненциальной сложностью) эффективными не являются. С учетом, например, того, что при 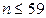справедливо неравенство 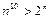, хотя 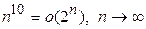, имеет смысл говорить об асимптотической сложности алгоритмов. Умножение функции сложности на константу принципиально не изменяет эту характеристику сложности задачи.

Значение разбиения задач на классы сложности становится понятным, если рассмотреть следующие практические соображения.

Пусть решая некоторую задачу Z на компьютере 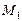можно было потратить Т единиц времени бесперебойной работы (без отказов, выключений и пр.). Переход на компьютер 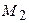с быстродействием в 10 раз большим можно считать эквивалентным увеличению времени бесперебойной работы в десять раз и равным 10Т. Если наибольшую размерность задачи, практически решаемой на компьютере 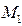обозначить 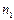, а на 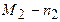, то для произвольной временной сложности 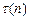-можно составить уравнение

,

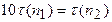разрешив которое относительно 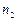, можно увидеть, на сколько может быть увеличена размерность решаемых задач при переходе на компьютер с большим на порядок быстродействием. Например, при 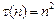получим: .

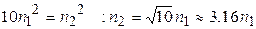Но если 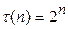, то 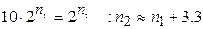. Практически это означает, например, что если удавалось решать некоторую задачу с матрицей размерности, не превышающей 100, на компьютере 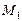и эта задача имеет экспоненциальную сложность, то, применив имеющий в 10 раз более быстродействие компьютер 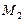, вам удастся увеличить размерность решаемой задачи всего лишь до 103.

Приведенная ниже таблица (заимствованная из [1]), ярко иллюстрирует значение функции сложности.

Временная сложность задачи	Наибольшая возможная размерность входа на имеющейся ЭВМ	Наибольшая возможная размерность входа на ЭВМ в 100 раз более быстрой	Наибольшая возможная размерность входа на ЭВМ в 1000 раз более быстрой
n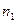

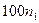
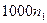
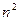
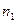
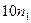
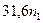
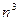
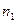
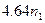
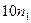
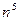
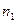
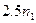
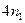
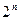
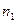
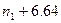
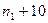
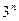
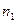
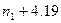
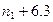
Недетерминированные алгоритмы и класс NP

Чтобы ввести сложное и являющееся примером исключительной абстракции понятие недетерминированного алгоритма, рассмотрим одну простую схему решения задачи коммивояжера в следующей постановке. Существует ли в данном конечном графе с заданными длинами дуг гамильтонов контур длины, не превышающий величины В? Напомним, что гамильтоновым контуром называют цикл в графе, проходящий каждую вершину ровно один раз

Если число вершин графа равно n, то число всех гамильтоновых контуров, очевидно, не превысит (п-1)!.

Тривиальный алгоритм, основанный на полном переборе, состоит в следующем.

1° УСПЕХ:= «FALSE»,

2° Выбрать очередной гамильтонов контор γ.

3° Вычислить его длину L(γ).

4° Если 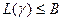, то { УСПЕХ:= «ТRUE»; перейти на 6°}.

5° Если перебор всех гамильтоновых контуров не закончен,

перейти на 2°.

6° Вывод значения переменной УСПЕХ.

Учитывая асимптотическое представление факториала

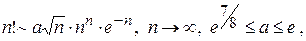
легко убедиться, что тривиальный алгоритм не является полиномиальным по сложности. Это типичный пример так называемого переборного алгоритма.

Для того, чтобы построить теорию сложности решения переборных дискретных задач, был предложен недетерминированный оператор «угадывания» отдельных элементов перебираемых множеств - допустимых решений, причем считается; что такай оператор, осуществляет выбор сразу всех возможных решений. Такая абстракция в какой-то степени соответствует представлению о распараллеливании алгоритмов.

Если Х - конечное множество допустимых решений некоторой задачи, то недетерминированный оператор CHOOSE(Х) осуществляет выбор х:=CHOOSE(Х) одновременно всех хÎХ, так что последующая алгоритмическая проверка некоторого свойства (предиката) Р(х) позволяет сделать вывод о его выполнимости или невыполнимости сразу на всем множестве X. Можно сказать, что если элемент с интересующими нас свойствами во множестве Х имеется, то недетерминированный оператор обязательно «угадает» этот элемент. Типичный пример недетерминированного алгоритма имеет вид:

Х:= СНОOSЕ (Х); // недетерминированный выбор

if Р(х) then write («УСПЕХ») // проверка свойства

еlse writе («НЕУДАЧА»);

Такие алгоритмы содержат два основных элемента: недетерминированный выбор и проверку свойства. Сложность недетерминированного алгоритма определяется только сложностью проверки свойства Р(х), сложность же перебора элиминируется недетерминированным оператором выбора, что и является трудно воспринимаемой абстракцией, но важнейшим для теории сложности обстоятельством.

Обычно моделью недетерминированной алгоритмической системы является недетерминированная машина Тьюринга (НДТМ). Однако мы будем использовать модель, более близкую к реальному ходу вычислений на современном однопроцессорном компьютере: алгоритмический язык, к которому добавлен недетерминированный оператор СНOOSЕ. Такой язык будем называть N-ALGOL и считать его расширением некоторого алгоритмического языка высокого уровня, условно названного ALGOL. Программу на языке N-ALGOL будем называть N-программой. Выполнение недетерминированного оператора СНООSЕ считается одним элементарным шагом.

Определение 4.2. Классом NР называется множество всех задач, для которых существует программа на языке N-ALGOL с полиномиальной временной сложностью, вычисляющая правильный ответ для любых допустимых вариантов исходных данных.

С точки зрения двухэтапности переборного алгоритма «выбор – проверка свойства», сложный переборный процесс выбора нужного элемента при определении класса NР не берется в расчет. От задач класса NР требуется только возможность полиномиальной по сложности проверки свойств. Поэтому класс NР часто называют классом задач с полиномиальной проверкой свойства.

Поскольку язык N-ALGOL является расширением языка ALGOL, то любая программа является N-программой, и выполняется включение рÌ nр. Справедливость равенства Р = nр сомнительна, поскольку оно повлекло бы существование полиномиальных алгоритмов для всех переборных задач. Поэтому соотношение Р¹ NР, подтверждаемое опытом математиков - вычислителей и специалистов в области теории алгоритмов и математической логики, считается гипотезой.