Лекция 2. Основные определения полиномиального сведения

1) Основные определения полиномиального сведения [1,2,3,4,5,6,7,8,9]

Ниже излагаются основы теории сложности, заложенной в работах С. Кука, Р. Карпа, А.А. Левина. Важно обратить внимание на полиномиальное преобразование задач как главный элемент этой теории. Известно, например, что задача о максимальном потоке в сети может быть преобразована в задачу линейного программирования. Подобные преобразования задач иногда оказываются полезными для нахождения решений, и для их осуществления в общем случае приходится производить некоторые вычисления, связанные с перекодированием и начальной информации, и ответа - решения задачи. Применение преобразований исходных задач, например, для их сведения к уже изученным задачам, решение которых известно, давно применяется математиками. Для дальнейшего изложения важно отметить, что нас будут интересовать полиномиальные по сложности алгоритмы сведения задач.

Будем далее рассматривать класс задач вычисления свойств. Задачи этого класса всегда имеют двузначный ответ: «да» или «нет». Например, к такому классу будет относиться задачи: существует ли в заданном конечном графе с указанными длинами ребер гамильтонов контур длины, не превышающей заданную величину, является ли выполнимой (тождественно неравной нулю) заданная формула алгебры логики, является ли данная правильно построенная формула некоторого исчисления теоремой в нем, существует ли решение задачи скалярной целочисленной оптимизации со значением целевой функции не меньшим указанной величины, является ли совместной заданная система линейных неравенств с целочисленными переменными и другие. Видно, что класс задач вычисления свойств достаточно широк.

Определение 4.3. Задачи (вычисления свойств) из множества Z полиномиально сводятся к задачам из множества S (обозначение - Zµ S), если существует функция j, вычислимая за полиномиальное время и преобразующая любую задачу zÎ Z в задачу j(z) = s, sÎ S, так, что задача z и задача s всегда дают совпадающий ответ: либо одновременно – «да», либо одновременно – «нет».

Рис. 4.1. Схема полиномиальной сводимости задачи Z к задаче j(z).

Рис. 4. поясняет, как можно воспользоваться полиномиальной сводимостью задачи z, которую нужно решить, к другой задаче s, относительно которой известно, что она легко решаема, например, с полиномиальной сложностью. Согласно схеме, приведенной на этом рисунке, два алгоритма должны быть выполнены последовательно, поэтому итоговая сложность такого двухэтапного решения является суммой сложности преобразования j и сложности решения задачи s=j(z). Сумма двух полиномов является полиномом, поэтому легко видеть, что если сложность решения задачи s=j(z) оценивается полиномом и сложность преобразования j являетсяполиномиальной, то задача z полиномиально разрешима.

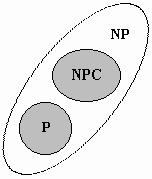
Определение 4.4. Задача Z* называется NР - полной (универсальной переборной задачей), если Z*Î NР и для любой задачи ZÎ NР имеет место полиномиальная сводимость Z µ Z*.

Множество всех NР - полных задач часто обозначают NPС (Nondeterministic Polynomial Compete). Из определения 4.2. следует, что NPС Ì NP и NP -полные задачи являются наиболее сложными в классе NP: если хотя бы одну NP -полную задачу удалось решить за полиномиальное время, то и все задачи из NP (в силу полиномиальной сводимости Z µ Z*) также удалось бы решить за полиномиальное время.