Тема 8. Матроиды и greedy алгоритмы

Пусть

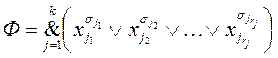
есть произвольная k скобочная КНФ. Поставим во взаимно-однозначное соответствие каждому литералу из Ф вершину некоторого графа Г. Этот граф будет содержать 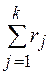вершин. Пометим для удобства каждую вершину соответствующим ей литералом и порядковым номером скобки, в которую этот литерал входит, т.е. парой

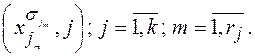
Соединим дугой те и только те пары полученных вершин 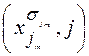и 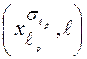, для которых одновременно выполняются два условия:

а) 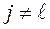(литералы принадлежат разным скобкам);

б) 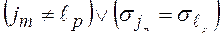(один литерал не является отрицанием другого).

Таким образом, построен граф Г =(X,U) с указанными вершинами и ребрами. Предположим, - что Ф – выполнима, и 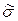-набор, на котором 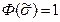. Тогда в каждом наборе КНФ Ф найдется хотя бы один литерал, обращающийся в единицу. Выберем произвольно по одному такому (обращающемуся в единицу) литералу из каждой скобки. Будет выбрано ровно k литералов. Рассмотрим соответствующие именно этим литералам k вершин графа Г и убедимся, что любая пара из них соединена ребром. Действительно, пометки этих вершин удовлетворяют условиям а) и б), т.к. литералы принадлежат разным скобкам и одновременно принимают единичное значение, поэтому один из них не может быть инверсией другого.

Обратно, пусть граф Г содержит полный подграф с k вершинами . зададим переменным с номерами 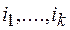значения: , а остальные переменные, если k < n, зададим произвольно, получая набор 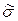. Тогда 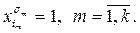Поскольку эти литералы соответствуют вершинам полного подграфа, то они относятся к разным скобкам КНФ Ф, откуда следует, что 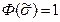. По построению графа Г очевидно, что преобразование задачи выполнимости КНФ в задачу 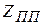может быть осуществлено с полиномиальной сложностью.

Теорема доказана.

Литература:

1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. – 416 с.

2. Ахо А., Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. – 536 с.

3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.

4. Донской В. И. Дискретная математика. –Симферополь: Сонат, 2000. –356 с.

5. Липский В. Комбинаторика для программистов. М.: Мир, 1988. – 215 с.

6. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физико-математическая литература, 1995. – 256 с

7. Линдон Р. Заметки по логике. М.: Мир, 1968. – 128 с.

8. Оре О. Теория графов. М.: Наука, 1980. – 336 с.

9. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.