Лекция 1. Теорема Радо-Эдмондса

1) Теорема Радо-Эдмондса [1,2,3,4,5,6,7,8,9]

Рассмотрим следующую задачу.

Задача 8.1. Дана матрица с целыми неотрицательными коэффициентами 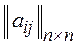. Требуется найти такое подмножество ее элементов, что: а ) в каждом столбце матрицы содержится не более одного элемента из этого подмножества и б) сумма выбранных элементов максимальна.

Эквивалентная формулировка этой задачи, очевидно, имеет вид:

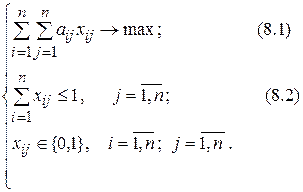
Будем решать задачу 8.1, отбирая последовательно элементы из 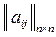, причем каждый раз - наибольший из оставшихся невыбранными, проверяя при этом выполнение ограничений (8.2). Алгоритмы такого типа называют жадными или пожирающими (в англоязычной литературе - GREEDY). Жадные алгоритмы похожи на градиентные алгоритмы в численных методах непрерывной математики.

Легко убедиться, что жадный алгоритм правильно решает задачу 9.1. Эта задача является индивидуальной задачей проблемы целочисленного линейного программирования (ЦЛП) с булевыми переменными и ограничениями, задание которых в этом частном случае определяет полиномиальную разрешимость задачи 9.1 со сложностью .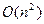

Для примера рассмотрим задачу 8.1 с матрицей

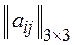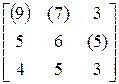Выбор наибольшего элемента в первом столбце 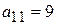в искомое подмножество исключает из дальнейшего рассмотрения (в силу заданного ограничения) элементы 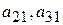. Из второго столбца выбирается 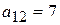и затем - из третьего столбца - 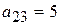. Имеем 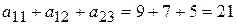. Это – точное экстремальное решение задачи. Скобками отмечены отобранные элементы.

Рассмотрим еще один частный случай задачи ЦЛП.

Задача 8.2. Дана матрица 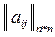с целыми неотрицательными коэффициентами. Найти такое подмножество ее элементов, что а ) в каждом столбце и в каждой строке находится не более одного выбранного элемента и б) сумма выбранных элементов является максимальной.

Эквивалентная формулировка задачи:

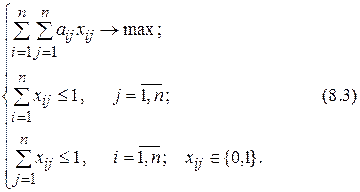
Попробуем применить жадный алгоритм к задаче (8.3) с матрицей

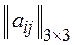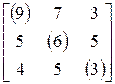Выбор наибольшего элемента в первой строке и столбце 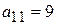в искомое подмножество исключает из дальнейшего рассмотрения (в силу заданных ограничений) элементы 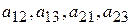. Поэтому из второго столбца выбирается 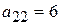и затем - из третьего столбца - 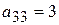. Имеем 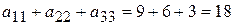. Но это решение не экстремальное: подмножество 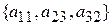удовлетворяет ограничениям и 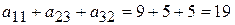. Укажем в матрице элементы экстремального решения:

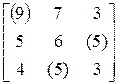Теперь рассмотрим более широкий, общий класс задач, включающий в себя задачи 9.1 и 9.2.

Задача 9.3. Дано конечное множество Е, семейство его подмножеств 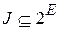(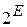- булеан множества Е) и функция w: Е ® R ⁺. Требуется найти подмножество SÎ J с наибольшей суммой .

Эквивалентная формулировка задачи 8.3:

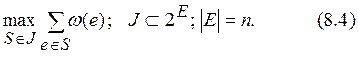
Значение функции w (е) будем называть весом элемента еÎ Е. Задача 8.3 может быть переформулирована так: найти допустимое подмножество SÎ J с наибольшим суммарным весом.