Оболочечная модель ядра

Модель жидкой капли и модель ферми-газа- очень грубые модели ядра. Хотя они и описывают важнейшие свойства ядер, они не могут объяснить специфических свойств их возбуждённых состояний. Бартлет[4], а затем Эльзассер[5] первыми обратили внимание на то, что ядра имеют особенно стабильные конфигурации, когда число Z или N (или оба эти числа) равно одному из магических чисел:

2, 8, 20, 28, 50, 82,. 126 (4.21)

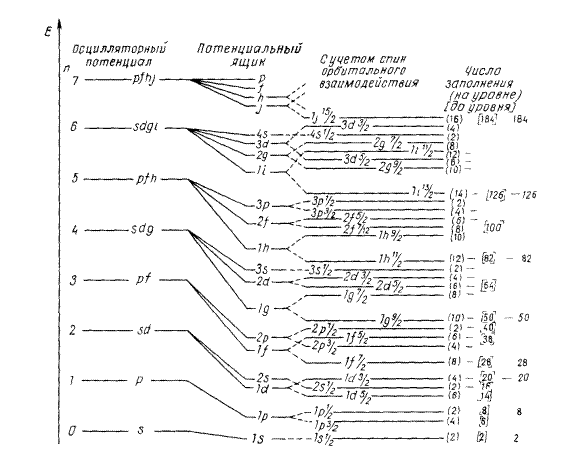
В 1947 г. магические числа удалось теоретически обосновать с помощью представления об одночастичных орбитах в ядрах. Это сделали М. Гепперт-Майер[6] и Дж. Иенсен[7]. Они сообразили, что для объяснения существования замкнутых оболочек с магическими числами 50, 82 и 126 следует учитывать спин-орбитальные взаимодействия. В простой модели ядерных оболочек предполагается, что нуклоны движутся независимо друг от друга сферически-симметричном потенциале ядра. При этом пренебрегают взаимодействием между отдельными нуклонами, но явно учитывают вид волновых функций нуклонов в эмпирическом усреднённом потенциале. Магические числа возникают из-за того, что энергетические уровни (как и в атомах) группируются в оболочки и полностью заполненные оболочки являются относительно стабильными образованиями. Термин «магические» исторически связан с тем, что в течение длительного времени не удавалось построить оболочки с нужными числами заполнения.

Оболочечная модель является следствием приближения Хартии-Фока, известного из атомной физики. В этом приближении сначала находят волновые функции отдельных фермионов в некотором усреднённом кулоновском поле других электронов, и из найденной таким образом плотности распределения заряда с помощью закона Кулона восстанавливают результирующий электростатический потенциал. Соответствующее число итераций позволяет найти такой потенциал с желаемой точностью и тем самым решить исходные интегральные уравнения.

Концепция усреднённого потенциала для ядер требует, однако, некоторых уточнений, поскольку ядерные силы на малых расстояниях между нуклонами очень резко зависят от расстояния. Рассмотрим этот вопрос подробнее. Оператор в уравнении Шредингера может быть представлен в виде суммы одночастичного и двухчастичных членов:

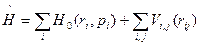. (4.22)

Это разбиение на одночастичный оператор и возмущение (двухчастичная часть) следует произвести так, чтобы второй оператор давал минимальный вклад, и этим вкладом можно было пренебречь. Волновая функция представляет собой антисимметризованную сумму

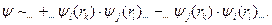
Каждый член этой суммы удовлетворяет невозмущённому уравнению Шредингера, если одночастичные функции являются решением своего уравнения. Вследствие требования антисимметрии одночастичные функции должны соответствовать различным состояниям.