Радиоактивность есть самопроизвольное изменение состава атомного ядра, происходящее за время, существенно большее характерного ядерного времени (10-23с). Время такого самопроизвольного изменения может варьироваться от времен порядка жизни вселенной (~1018сек) до времен доступных для современных регистраторов (~10-12с). Распады ядер часто происходят значительно быстрее, но такие распады уже не принято относить к радиоактивным.
Ядра, подверженные радиоактивным превращениям, называются радиоактивными, а не подверженные- стабильными. Такое деление условно, так как, в сущности, все ядра могут самопроизвольно распадаться, но этот процесс в разных ядрах идет с различной скоростью.
Различают следующие виды радиоактивного распада:
· a-распад (испускание ядром a-частицы (ядра 4He) с энергией ~5-7 МэВ и поглощающейся несколькими микронами алюминия). При a-распаде зарядовое число ядра уменьшается на две единицы и образуется новый элемент, сдвинутый относительно исходного влево на две клети периодической системы;
|
|
|
· b-распад. Бета-распад может быть трех видов: 1) электронный или b--распад; 2) позитронный или b+-распад; 3) электронный захват.;
· Спонтанное деление атомного ядра, т. е. самопроизвольный распад тяжелого ядра на два близких по массе осколка. Спонтанное деление было открыто советскими физиками Г. Флеровым и К. Петржаком в 1940 г. Примером может служить процесс 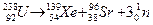 ;
;
· Протонный распад и двухпротонная радиоактивность у ядер с большим избытком протонов;
· Ядерная изомерия (процесс испускания ядром g -квантов из долгоживущих изомерных состояний);
· Запаздывающая нейтронная, протонная, и a -радиоактивность. Эта радиоактивность сопровождает b-распад;
· Кластерная радиоактивность. Обнаружена в Оксфорде в 1984 г. Характеризуется испусканием тяжелыми ядрами нуклонных ассоциаций более тяжелых чем a-частицы, но более легких чем осколки деления. Пример 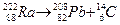 .
.
Единицей активности является Кюри -1Ku=3,700×1010распадов/сек.
Естественная единица активности 1Беккерель – 1Бк=1распад/сек.
В литературе можно также встретить единицу –резерфорд
1Рд=106Бк
В процессе радиоактивного распада должны выполняться законы сохранения (энергии, импульса, момента импульса, электрического, барионного и лептонного зарядов и пр.). В частности для закона сохранения энергии, если ядро неподвижно, можно написать
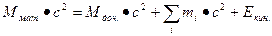 , (5.1)
, (5.1)
где Mмат. и Mдоч. – массы начального (материнского) и конечного (дочернего) ядер, m i – массы испущенных частиц, Eкин. – кинетическая энергия продуктов радиоактивного распада. Так как самопроизвольно могут идти только реакции с выделением энергии, а потому энергия Е сугубо положительна. Таким образом, радиоактивный распад возможен лишь тогда, когда выполняется условие 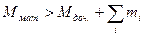 . Это условие необходимое, но недостаточное, так как для реализации процесса, помимо закона сохранения энергии, должны выполняться и другие законы сохранения.
. Это условие необходимое, но недостаточное, так как для реализации процесса, помимо закона сохранения энергии, должны выполняться и другие законы сохранения.
|
|
|
5.2. Закон радиоактивного распада.
Из эксперимента известно, что скорость радиоактивного распада прямо пропорциональна числу распадающихся ядер в наблюдаемый момент времени 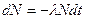 . Знак минус означает, что число ядер убывает во времени. Поскольку l не зависит от времени, после интегрирования получаем
. Знак минус означает, что число ядер убывает во времени. Поскольку l не зависит от времени, после интегрирования получаем

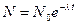 (5.2)
(5.2)
Здесь N0 -число ядер в начальный момент времени, а l - постоянная распада для радиоактивных ядер данного сорта. Постоянную распада l можно выразить через среднее время жизни радиоактивного ядра. Оно вытекает из выражения
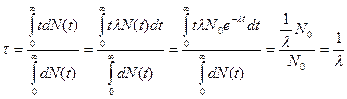 . (5.3)
. (5.3)
Время Т 1/2, по истечении которого число наличных радиоактивных атомов убывает в два раза, называется периодом или временем полураспада.
Период полураспада может быть получен из условия
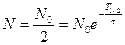 . Откуда T 1/2=tln2=0,6931t. (5.4)
. Откуда T 1/2=tln2=0,6931t. (5.4)
Если одновременно происходят два конкурирующих процесса, так что ядра N могут одновременно испускать частицы одного сорта N1, согласно уравнению dN1=-l1Ndt, и частицы другого сорта N2, согласно уравнению dN2=-l2Ndt, то
dN=dN1+ dN2=-(l1+l2)Ndt.
Отсюда следует, что обратная величина «результирующего» времени жизни t равна сумме обратных величин времен жизни t1 и t2 обоих конкурирующих процессов: 1/t=1/t2+1/t1.
При радиоактивном распаде ядер исходного вещества, как правило, возникают новые радиоактивные ядра. В таком случае исходные ядра называются материнскими, а получающиеся при распаде- дочерними. При этом 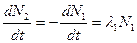 . В случае, когда дочернее ядро также радиоактивно с постоянной распада l2, количество дочерних ядер подчиняется выражению
. В случае, когда дочернее ядро также радиоактивно с постоянной распада l2, количество дочерних ядер подчиняется выражению
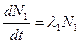 ;
; 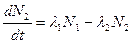 . (5.5)
. (5.5)
Решение системы уравнений (5.5) имеет вид:
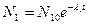 ,
, 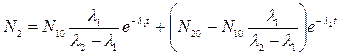 , (5.6)
, (5.6)
где N10 и N20 –начальные значения чисел атомов N1 и N2 материнского и дочернего вещества. В частном случае, когда в начальный момент дочернее вещество ещё не образовалось (N2 =0), формула (5.6) упрощается и переходит в
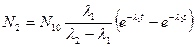 (5.7)
(5.7)
Особенно важным является случай, когда материнское вещество- долгоживущее, а дочернее вещество по сравнению с ним распадается быстро (l1<<l2). Если время t таково, что (l1t <<1), то изменением N1 можно пренебречь. В таком случае из (5.6) и (5.7) получается
N 1=const, 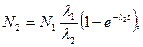 (5.8)
(5.8)
Число атомов N2 при t ® ∞ асимптотически стремится к насыщению N2 (∞)= N1 ·l1/l2. Таким образом, в состоянии насыщения выполняется условие (l1· N1 =l2· N1). Это равенство называют также условием радиоактивного равновесия.
На основе закона радиоактивного распада работают «атомные часы», служащие в некоторых случаях, например в геологии или археологии, для измерения промежутков времени.
Для оценки возраста мертвых организмов (древесины, костей животных и пр.), не превышающего примерно 50000 лет, используется радиоактивный изотоп 14С. Испытывая b--распад, он превращается в азот 14N. Период полураспада для 14С составляет Т1/2 =5570 лет. Радиоактивный углерод образуется за счет ядерных реакций (15N+g ® 14С+р) в верхних слоях атмосферы и во всех живых организмах его доля по отношению к стабильным изотопам постоянна и соответствует соотношению в атмосфере. Если предположить, что поток гамма-лучей за последние 50-60 тысяч лет не изменился, то изменение отношения 14С/12С в ископаемом образце относительно эталонного (современного) даст нам возможность оценить древность находки.
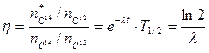 . Здесь
. Здесь 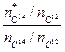 отношение 14С/12С для анализируемого вещества и эталона.
отношение 14С/12С для анализируемого вещества и эталона.
Отсюда получаем для искомого времени 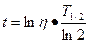 .
.
Задача: В настоящее время в природном уране содержится 99,274% 238U (Т1/2=4,5·109лет) и 0,72% 235U (Т1/2 =7,04·108лет). Вычислить возраст Земли (солнечной системы) в предположении, что в момент образования Земли количества 238U и 235U были одинаковы.
Ответ: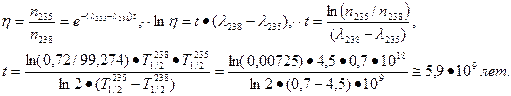
 2014-02-13
2014-02-13 3075
3075
