Содержание отчета к заданию.
Задание для выполнения контрольной работы.
Сравнение погрешности квадратичных формул.
Точность квадратурной формулы характеризуется порядком остаточного члена степени шага интегрирования.
Итак, остаточные члены формул левых и правых прямоугольников относительно h имеют первый порядок: R(f)=O(h), средних прямоугольников и трапеций – второй: R(f)=O(h²), а Симпсона – четвертый: R(f)=O(h4). Квадратурную формулу считают тем точнее, чем больше порядок ее остаточного члена R(f). Из рассмотренных ранее квадратурных формул самой точной является формула Симпсона, а наименее точными – формулы левых и правых прямоугольников. Точность формул средних прямоугольников и трапеций одинакова.
Варианты заданий изложены в таблице 2.
1. Построить алгоритм вычисления приближенного значения интеграла по обобщенной формуле указанной в табл.2 и составить соответствующий алгоритм вычисления в среде табличного процессора Excel.
|
|
|
2. Используя этот алгоритм вычислить значение интеграла на указанном отрезке интегрирования [a;b], разделив отрезок на N0 равных частей, оценить остаточный член.
3. Сравнить вычисленное значение интеграла с тем значением, которое получают путем непосредственного интегрирования.
Таблица 2 - варианты функций численного интегрирования.
| Вариант | 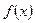
| a | B | N0 | Формула |
| 1. | 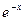
| прямоугольников | |||
| 2. | 
| прямоугольников | |||
| 3. | 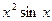
| прямоугольников | |||
| 4. | 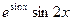
| прямоугольников | |||
| 5. | 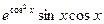
| прямоугольников | |||
| 6. | 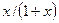
| прямоугольников | |||
| 7. | 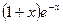
| прямоугольников | |||
| 8. | 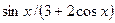
| прямоугольников | |||
| 9. | 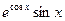
| прямоугольников | |||
| 10. | 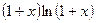
| прямоугольников | |||
| 11. | 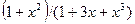
| трапеций | |||
| 12. | 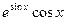
| трапеций | |||
| 13. | 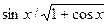
| трапеций | |||
| 14. | 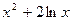
| трапеций | |||
| 15. | 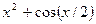
| трапеций | |||
| 16. | 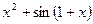
| трапеций | |||
| 17. | 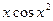
| трапеций | |||
| 18. | 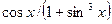
| трапеций | |||
| 19. | 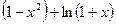
| трапеций | |||
| 20. | 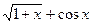
| трапеций | |||
| 21. | 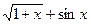
| Симпсона | |||
| 22. | 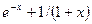
| Симпсона | |||
| 23. | 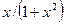
| Симпсона | |||
| 24. | 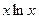
| Симпсона | |||
| 25. | 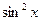
| 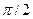
| Симпсона | ||
| 26. | 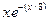
| Симпсона | |||
| 27. | 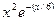
| Симпсона | |||
| 28. | 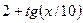
| Симпсона | |||
| 29. | 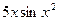
| Симпсона | |||
| 30. | 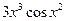
| Симпсона |
В отчете необходимо предъявить:
- решение задания;
· оценку погрешности численного интегрирования;
- алгоритм решения задания в среде табличного процессора Excel;
- файл, содержащий реализацию использованных методов в среде табличного процессора Excel;
· анализ результатов и выводы.
|
|
|
Пример выполнения задания.
Используя метод Симпсона вычислить:
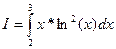
При вычислении разбить отрезок интегрирования на 8 частей. Оценить погрешность вычисления по остаточному члену. Вычисления организовать в среде табличного процессора Excel.
Получить аналитическое выражение для указанного интеграла и рассчитать его значение. Сравнить точное значение с результатом вычисления методом Симпсона, сделать вывод.
 2014-02-17
2014-02-17 410
410








