В процессе функционирования сети Петри некоторые ее места могут накапливать неограниченное число фишек. Примером такого места может служить место 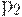 в сети на рис.8.6. Если интерпретировать места как
в сети на рис.8.6. Если интерпретировать места как
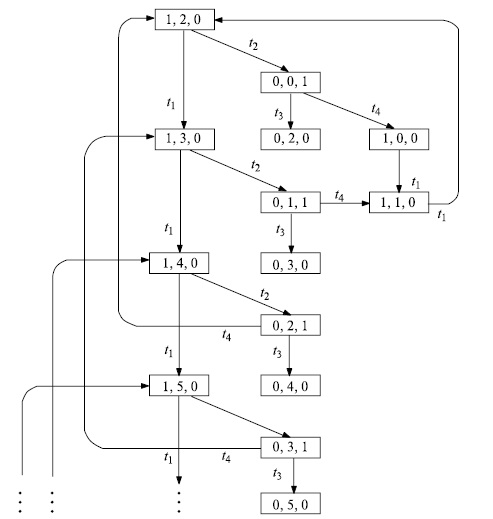
Рис. 8.7. Граф разметок сети Петри
накопители (буферы) данных, сигналов или деталей в моделируемых системах, то естественно потребовать, чтобы при любом варианте функционирования этих систем не происходило переполнение накопителей, которые в реальных ситуациях имеют конечную, фиксированную емкость. Следующие понятия формализуют такие требования.
Определение. Место 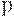 в сети Петри
в сети Петри 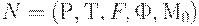 называется ограниченным, если существует число
называется ограниченным, если существует число 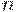 , такое что для любой достижимой в сети разметки
, такое что для любой достижимой в сети разметки 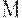 справедливо неравенство
справедливо неравенство 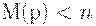 . Сеть
. Сеть 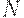 называется ограниченной сетью, если любое ее место ограничено.
называется ограниченной сетью, если любое ее место ограничено.
Ясно, что множество достижимых разметок 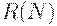 конечно, если и только если
конечно, если и только если 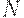 - ограниченная сеть. В сети на рис.8.6 места
- ограниченная сеть. В сети на рис.8.6 места 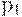 , и
, и 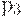 ограничены, так как каждое из них может содержать не более одной фишки. В то же время место
ограничены, так как каждое из них может содержать не более одной фишки. В то же время место 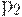 не ограничено, и поэтому эта сеть не является ограниченной.
не ограничено, и поэтому эта сеть не является ограниченной.
Определение. Место 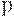 называется безопасным, если для всякой достижимой разметки
называется безопасным, если для всякой достижимой разметки 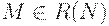 выполняется неравенство
выполняется неравенство 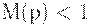 ; соответственно, сеть безопасна, если все ее места безопасны.
; соответственно, сеть безопасна, если все ее места безопасны.
Любая достижимая в безопасной сети разметка представляет собой вектор из 0 и 1. Сеть, показанная на рис.8.6, не является безопасной.
Родственным понятиям ограниченной и безопасной сети Петри является понятие консервативной, или сохраняющей, сети.
Определение. Сеть, в которой сумма фишек во всех ее местах остается постоянной в процессе работы сети, то есть
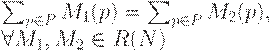
называется сохраняющей (консервативной).
Условие сохранения числа фишек в сети - это очень сильное ограничение. Например, из него немедленно следует, что число входов в каждый переход должно равняться числу выходов (с учетом кратности). Если бы это было не так, запуск перехода изменил бы число фишек в сети.
Часто фишки в сети Петри моделируют различные ресурсы. Однако взаимно однозначного соответствия между фишками и ресурсами нет. Фишка может представлять как один ресурс, так и несколько ресурсов сразу. Во втором случае фишка может использоваться для создания кратных фишек (по одной на ресурс) путем запуска перехода с большим числом выходов, чем входов. Поэтому определение свойства сохраняемости сети целесообразно сделать более общим, заменив простую сумму фишек на сумму с весами. Фишкам, не являющимся важными, можно присвоить нулевой вес; другим фишкам можно присвоить весы 1, 2, 3 или любое другое положительное число.
Определение. Сеть Петри называется сохраняющей (консервативной) по отношению к вектору весов 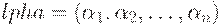 , где
, где 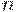 - число мест в сети, если
- число мест в сети, если
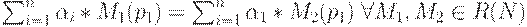 | (8.6) |
Сохраняющая сеть Петри является сохраняющей по отношению к вектору весов 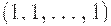 . Следует исключить из рассмотрения нулевой вектор весов, поскольку все сети являются сохраняющими по отношению к нулевому вектору весов.
. Следует исключить из рассмотрения нулевой вектор весов, поскольку все сети являются сохраняющими по отношению к нулевому вектору весов.
Переходы в сетях Петри, как правило, моделируют некоторые действия (события), которые могут совершаться в реальных процессах обработки. Поэтому вопросы, касающиеся возможности срабатывания тех или иных переходов, представляют интерес при анализе сетей Петри.
Переход в сети может сработать при определенных условиях, связанных с разметкой его входных мест. Может оказаться, что для некоторого перехода условие его срабатывания никогда не выполняется, как бы ни функционировала сеть. Такой переход - лишний в сети, его можно исключить без ущерба для работы сети. Может случиться также, что после некоторой последовательности срабатываний переходов сети и соответствующих изменений ее разметки некоторые переходы, в том числе те, которые уже срабатывали, больше никогда не сработают, какие бы варианты достижимых в сети разметок не возникали. Это означает, что в моделируемых системах могут появляться ситуации, тупиковые для некоторых событий. Например, в операционных системах подобные случаи происходят при взаимных блокировках процессов (deadlocks) при недоступности требуемых ресурсов. Таким образом, переходы в сети Петри могут обладать различной активностью, и их можно разбить на категории по уровню активности.
Уровень 0: переход 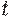 обладает активностью уровня 0 и называется мертвым, если он никогда не может быть запущен.
обладает активностью уровня 0 и называется мертвым, если он никогда не может быть запущен.
Уровень 1: переход 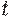 обладает активностью уровня 1 и называется потенциально живым, если существует такая разметка
обладает активностью уровня 1 и называется потенциально живым, если существует такая разметка 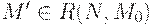 , что
, что 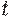 разрешен в
разрешен в 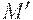 . Уровень 2: переход
. Уровень 2: переход 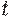 обладает активностью уровня 2, если для всякого целого
обладает активностью уровня 2, если для всякого целого 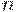 существует последовательность запусков, в которой
существует последовательность запусков, в которой 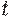 присутствует по крайней мере
присутствует по крайней мере 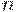 раз.
раз.
Уровень 3: переход 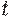 обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой
обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой 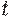 присутствует неограниченно часто.
присутствует неограниченно часто.
Уровень 4: переход 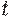 обладает активностью уровня 4 и называется живым, если для всякой
обладает активностью уровня 4 и называется живым, если для всякой 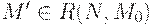 переход
переход 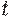 является потенциально живым для сети Петри
является потенциально живым для сети Петри 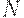 с начальной маркировкой
с начальной маркировкой 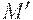 .
.
Сеть Петри называется живой, если все ее переходы являются живыми.
В качестве примера, иллюстрирующего уровни активности, рассмотрим сеть Петри на рис.8.8. Переход 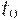 не может быть запущен никогда; он мертвый. Переход
не может быть запущен никогда; он мертвый. Переход 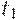 можно запустить только один раз; он обладает активностью уровня 1. Переход
можно запустить только один раз; он обладает активностью уровня 1. Переход 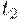 может быть запущен произвольное число раз, но это число зависит от числа запусков перехода
может быть запущен произвольное число раз, но это число зависит от числа запусков перехода 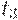 . Если мы хотим запустить
. Если мы хотим запустить 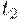 пять раз, мы запускаем пять раз
пять раз, мы запускаем пять раз 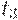 , затем
, затем 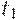 и после этого пять раз
и после этого пять раз 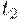 . Однако, как только запустится
. Однако, как только запустится 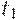 (
(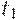 должен быть запущен до того, как будет запущен
должен быть запущен до того, как будет запущен 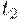 ), число возможных запусков
), число возможных запусков 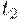 станет фиксированным. Следовательно,
станет фиксированным. Следовательно, 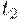 обладает активностью уровня 2, но не уровня 3. С другой стороны, переход
обладает активностью уровня 2, но не уровня 3. С другой стороны, переход 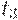 можно запускать бесконечное число раз, и поэтому он обладает активностью уровня 3, но не уровня 4, поскольку, как только запустится
можно запускать бесконечное число раз, и поэтому он обладает активностью уровня 3, но не уровня 4, поскольку, как только запустится 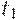 , переход
, переход 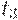 больше запустить будет нельзя.
больше запустить будет нельзя.
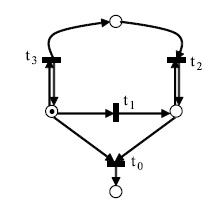
Рис. 8.8. Сеть Петри, иллюстрирующая различные уровни активности переходов
Многие прикладные задачи анализа систем и процессов в терминах сетей Петри могут быть сформулированы как задача о достижимости заданной разметки сети. Эта разметка может соответствовать целевому состоянию, в которое желательно перевести систему или процесс, или наоборот, описывать состояние, попадания в которое лучше избежать (аварийное, убыточное и т.п.). Важность задачи о достижимости заключается также в том, что к ней сводятся некоторые другие задачи анализа сетей Петри.
Формально задача о достижимости состоит в следующем: для сети Петри 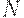 с начальной разметкой
с начальной разметкой 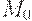 и заданной разметки
и заданной разметки 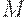 установить справедливость включения
установить справедливость включения 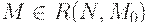 . Иными словами, требуется выяснить, существует ли допустимая последовательность срабатываний переходов
. Иными словами, требуется выяснить, существует ли допустимая последовательность срабатываний переходов 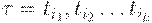 , переводящая сеть Петри из начальной разметки
, переводящая сеть Петри из начальной разметки 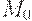 в заданную разметку
в заданную разметку 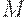 , то есть
, то есть 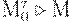 .
.
Близкой по смыслу к задаче о достижимости является задача о покрываемости. Она заключается в том, чтобы для данной сети Петри 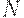 с начальной маркировкой
с начальной маркировкой 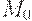 и заданной маркировки
и заданной маркировки 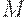 определить, существует ли такая достижимая маркировка
определить, существует ли такая достижимая маркировка 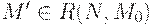 , что
, что 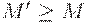 .
.
Напомним, что отношение 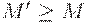 истинно, если каждый элемент маркировки
истинно, если каждый элемент маркировки 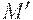 не меньше соответствующего элемента маркировки
не меньше соответствующего элемента маркировки 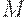 .
.
 2014-02-17
2014-02-17 933
933








