Лекция № 8
В настоящей главе рассмотрены процедуры вывода в логике предикатов первого порядка, позволяющие осуществлять вывод целевых формул. Введены основные понятия исчисления логики предикатов, отличающих его от исчисления высказываний. Продолжается знакомство с более сложными понятиями логических исчислений, базирующихся на логике предикатов первого порядка, показаны различные типы выводов. В конце главы затронуты вопросы полноты и непротиворечивости исчислений, основанных на логике предикатов первого порядка.
Во второй главе определено понятие и изложена суть вывода (поиска, рассуждения) в пространстве состояний с использованием логики высказываний. В третьей главе рассмотрен язык логики предикатов первого порядка, существенно более выразительный по сравнению с логикой высказываний. Это большая выразительность языка логики предикатов объясняется следующим. Вместо логических переменных логики высказываний в логике предикатов используются предикаты. Предикаты могут не иметь аргументов и тогда они являются полным аналогом логических переменных. Но предикаты могут иметь в качестве аргументов объектные константы и переменные, область значений которых может быть в принципе даже бесконечной. Истинностное значение предикатов в этом случае зависит от значения его аргументов. Кроме того, в логике предикатов используются кванторы, которые позволяют делать высказывания в лаконичной форме о множествах связанных определенными отношениями объектных переменных. Следствием большей выразительности языка логики предикатов является более сложная, хотя и схожая с логикой высказываний структура вывода.
4.5.1. Исчисление предикатов первого порядка
В главе 2 было определено понятие логического исчисления. Одним из таких исчислений является классическое исчисление предикатов. Как и любое другое исчисление, оно построено на использовании:
алфавита (совокупности используемых символов);
синтаксических правил построения формул в алфавите;
аксиом (общезначимых исходных формул);
правил вывода по аксиомам производных формул или теорем.
Алфавит и синтаксические правила построения формул в исчислении предикатов определены в предыдущей главе. Множество аксиом классического исчисления предикатов определяется следующим образом: каждая аксиома классического исчисления высказываний трансформируется в аксиому классического исчисления предикатов. Эта трансформация выражается только в том, что все ее логические переменные рассматриваются как предикаты, а формулы как формулы логики предикатов первого порядка.
К этому множеству аксиом, являющихся аналогом аксиом классического исчисления высказываний, добавляются две следующие аксиомы:
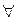 (х)
(х) (х)
(х) 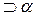 (у),
(у),
 (y)
(y) 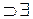 (х)
(х) (x).
(x).
Общезначимость этих аксиом легко проверить с помощью таблиц истинности.
Множеством правил классического исчисления предикатов является модус поненс 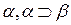 ├
├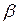 , в котором аир являются формулами логики предикатов первого порядка, и два правила введения кванторов:
, в котором аир являются формулами логики предикатов первого порядка, и два правила введения кванторов:
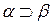 ├
├ 
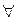 (x)
(x)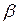 (x),
(x),
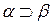 ├
├ 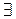 (x)
(x)  (x)
(x) 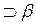 .
.
Классическое исчисление предикатов первого порядка не единственно. Существует множество других исчислений, построенных на основе классического, но использующих, помимо правил классического исчисления предикатов, и другие правила. В частности, в главе 2 были введены такие правила вывода в логике высказываний, как исключение конъюнкта, введение конъюнкции, исключение двойного отрицания, простая резолюция, резолюция. Эти правила справедливы и для логики предикатов, с тем только отличием, что в них используются формулы логики предикатов, а не логики высказываний.
Как и в случае классического исчисления высказываний, все аксиомы классического исчисления предикатов не содержат констант. Кроме того, все предикатные символы в классическом исчислении высказываний являются абстрактными в том смысле, что любой предикатный символ в аксиомах логического исчисления предикатов может быть переименован и от этого ничего не изменится. Иными словами, аксиомы классического исчисления предикатов, как и аксиомы классического исчисления высказываний, остаются аксиомами при любой интерпретации.
При использовании классического исчисления предикатов для описания свойств какой-либо конкретной среды абстрактные предикатные символы заменяют конкретными, называемыми также индивидуальными предикатными символами. Кроме того, вводят факты, аксиомы и правила, не являющиеся аксиомами классического исчисления предикатов и зависящие от той среды, для которой осуществляется формализация постановки задачи. В результате получается некоторое новое логическое исчисление. Формулы этого исчисления по-прежнему строят по тем же правилам, показанным на рис. 3.1. С его помощью можно выводить формулы, которые нельзя получить в классическом исчислении высказываний. С практической точки зрения нас интересуют именно такие исчисления, учитывающие особенности конкретных сред. В дальнейшем ряд таких исчислений и будет рассмотрен. Чтобы отличать такие исчисления от классического исчисления логики предикатов первого порядка, назовем их неклассическими исчислениями. К их числу относятся также исчисления, которые строятся не на основе логики предикатов первого порядка. В настоящей главе продолжим изучение неклассических исчислений, построенных на основе логики предикатов первого порядка.
Пусть, например, среди множества аксиом в неклассическом исчислении для какой-либо среды имеется две аксиомы 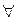 (x)
(x) (х) и
(х) и  (A)
(A)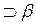 (В), где х — переменная; А, В — константы;
(В), где х — переменная; А, В — константы; 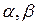 — предикатные символы. Спрашивается, можно ли на основании этих аксиом, используя правило модус поненс
— предикатные символы. Спрашивается, можно ли на основании этих аксиом, используя правило модус поненс 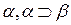 ├
├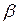 , заключить, что формула
, заключить, что формула 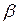 (В) истинна. Если принять
(В) истинна. Если принять 
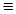
 (А),
(А), 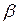
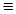
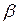 (B), то такое заключение можно было бы сделать, если бы среди исходных аксиом имелась аксиома
(B), то такое заключение можно было бы сделать, если бы среди исходных аксиом имелась аксиома  (А). Ее у нас нет. Имеется только аксиома
(А). Ее у нас нет. Имеется только аксиома 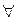 (x)
(x) (х). Эта аксиома гласит: «Для всех х имеет место истинность формулы
(х). Эта аксиома гласит: «Для всех х имеет место истинность формулы  (х)». Когда речь идет о всех х формулы
(х)». Когда речь идет о всех х формулы  (х), то имеются в виду, естественно, только те х, областью значений которых являются заранее оговоренные константы, среди которых есть константа А хотя бы потому, что она встречается в предикате
(х), то имеются в виду, естественно, только те х, областью значений которых являются заранее оговоренные константы, среди которых есть константа А хотя бы потому, что она встречается в предикате  (A) формулы
(A) формулы  (A)
(A) 
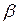 (B), т.е. в предикате, предикатный символ а которого совпадает с предикатным символом предиката в аксиоме
(B), т.е. в предикате, предикатный символ а которого совпадает с предикатным символом предиката в аксиоме 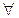 (x)
(x) (х). Это означает, что предикат
(х). Это означает, что предикат  (A) истинен. Следовательно, можно воспользоваться правилом модус поненс и заключить, что формула
(A) истинен. Следовательно, можно воспользоваться правилом модус поненс и заключить, что формула 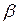 (B) истинна. Таким образом, чтобы воспользоваться правилом модус поненс
(B) истинна. Таким образом, чтобы воспользоваться правилом модус поненс
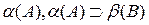 ├
├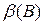 ,
,
пришлось по аксиоме 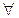 (x)
(x) (х) получить аксиому
(х) получить аксиому  (A). Это равносильно использованию правила вывода, означающего, что при наличии аксиомы
(A). Это равносильно использованию правила вывода, означающего, что при наличии аксиомы 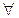 (x)
(x) (х) вместо переменной х в предикат
(х) вместо переменной х в предикат  (x) можно подставить константу А (эта подстановка обозначается х → А) и в результате получить аксиому
(x) можно подставить константу А (эта подстановка обозначается х → А) и в результате получить аксиому  (A). Это правило называют правилом исключения квантора общности. Кроме этого правила могут потребоваться также правила исключения квантора существования, которые записывают вобщем виде следующим образом:
(A). Это правило называют правилом исключения квантора общности. Кроме этого правила могут потребоваться также правила исключения квантора существования, которые записывают вобщем виде следующим образом:
 2014-02-09
2014-02-09 2234
2234








