Обобщенно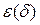е правило модус поненс

Обозначим некоторый атом, имеющий предикатный символ 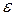и множество вхождений переменных и констант 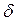. Тогда обобщенное правило модус поненс принимает вид

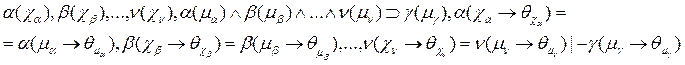
Смысл этого правила состоит в следующем. Формулы 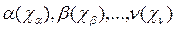являются атомами и каждый из них имеет множество вхождений констант и переменных 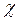. В формуле 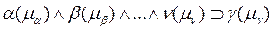, представленной импликацией, 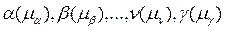являются атомами, каждый из которых имеет множество вхождений констант и переменных 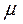. Если существуют подстановки 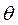такие, что

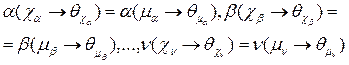то будет истинным атом .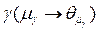

Напомним, что 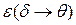означает, что вместо аргументов 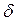атома 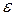подставляются аргументы 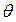. При этом необходимо соблюдать следующие требования:

Вместо переменной в 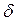можно подставлять переменную из 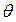. Такую подстановку называют переименованием переменной.

Вместо переменной в 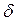можно подставлять константу из 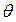. Такую подстановку называют конкретизацией переменной.

Вместо переменной в 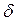можно подставлять функцию из 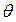. Такую подстановку называют заменой переменной.

Вместо одной и той же переменной везде следует подставлять одну и ту же константу или функцию. Переименовываются одновременно все вхождения одной и то же переменной.

Процесс поиска нужной подстановки 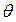называют унификацией, а формулу, в атомы которой осуществлена подстановка, называют унифицированной. В некоторых исчислениях для подстановки, конкретизации и замены переменной вводят отдельные правила. Подстановка называется наиболее общей, если благодаря ей наименьшее число переменных замещается константами. В обобщенном правиле модус поненс вместо 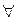(х)(х) записывают (х), т.е. кванторы общности подразумеваются, но не употребляются. Кванторы существования в обобщенном правиле модус поненс вообще не используются. Поскольку обобщенное правило модус поненс является единственным, которое мы собираемся использовать в процессе вывода, то, следовательно, постановка задачи изначально должна удовлетворять следующим условиям.

Формулы в постановке задачи не должны содержать кванторов существования.

Если они все же есть, то, прежде чем решать задачу, от кванторов существования следует избавиться с помощью, например, правила исключения квантора существования или какими-либо другими способами, речь о которых пойдет дальше.

Все формулы в постановке задачи должны быть атомами или импликациями, левая часть (посылка) которых является конъюнкцией атомов, а правая (заключение) — либо атомом, либо пустым символом.

Такие формулы называют хорновскими формулами.

Преобразование произвольных формул логики предикатов в хорновские формулы непростая задача, причем не любую формулу можно преобразовать к такому виду. В нашем примере со средой чудовища кванторов существования, не считая формулы цели, вообще нет, тем не менее, подобное преобразование всех формул невозможно. Например, это нельзя сделать для формул (4.18), (4.19). Рассмотрим, как выполняется указанное преобразование для формул (4.1) — (4.32). Для того чтобы можно было легко сопоставить эти формулы с их преобразованиями, будем последние нумеровать теми же числами, но со звездочкой, комментируя производимые преобразования (если в преобразованиях нет необходимости, то соответствующая формула переписывается без комментариев):

находится (Агент, 1,1), (4.1)*

ориентация (1, 2). (4.2)*

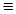
Выполняя преобразования на основе закона Ложь 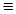Ложь, получаем

находится (Зловоние, 1, 1) Ложь, (4.3)*

находится (Сквозняк, 1,1) Ложь, (4.4)*

находится (Яма, 1, 1) Ложь. (4.5)*

Простым удалением квантора обшности (если он есть) или на основе закона

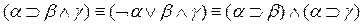получаем следующие формулы:

находится (Препятствие, i, 0), (4.6)*

находится (Препятствие, 0, j), (4.7)*

находится (Агент, 1, 2) находится (Зловоние, 1, 2), (4.8)*

находится (Агент, 2, 1) находится (Сквозняк, 2, 1),

находится (Агент, 2, 1) находится (Зловоние, 2, 1), (4.9)*

находится (Агент, 2, 3) находится (Блеск, 2, 3). (4.10)*

Выполняя преобразования на основе закона 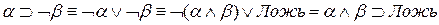, получаем следующие формулы:

находится (Агент, 1, 2) находится (Сквозняк, 1,2) Ложь, (4.11)*

находится (Агент, 2, 2) находится (Зловоние, 2, 2) Ложь, (4.12)*

находится (Агент, 2, 2) находится (Сквозняк, 2, 2) Ложь. (4.13)*

Вторая формула в (4.9)* может быть преобразована аналогично.

С помощью преобразования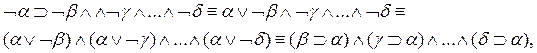

удаления квантора существования и правила исключения конъюнкта, получаем следующие формулы:

находится (Чудовище, i, j) находится (Зловоние, i, j),

находится (Чудовище, i, j-1) находится (Зловоние, i, j),

находится (Чудовище, i,j+1) находится (Зловоние, i,j),

находится (Чудовище, i-1, j) находится (Зловоние, i,j),

находится (Чудовище, i+1, j) находится (Зловоние, i,j); (4.14)*

находится (Яма, i, j) находится (Сквозняк, i, j),

находится (Яма, i, j-1) находится (Сквозняк, i, j),

находится (Яма, i, j + 1) находится (Сквозняк, i, j),

находится (Яма, i-1, j) находится (Сквозняк, i, j),

находится (Яма, i+1, j) находится (Сквозняк, i, j); (4.15)*

находится (Зловоние, i, j) находится (Чудовище, i, j),

находится (Зловоние, i, j-1) находится (Чудовище, i, j),

находится (Зловоние, i, j +1) находится (Чудовище, i,j),

находится (Зловоние, i-1,j) находится (Чудовище, i, j),

находится (Зловоние, i+1,j) находится (Чудовище, i, j). (4.16)*

Следующие формулы преобразовать к требуемому виду невозможно. Оставим их в прежнем виде, исключив квантор существования:

находится (Чудовище, i, j) находится (Зловоние, i, j)

находится (Зловоние, i, j-1) находится (Зловоние, i, j)

находится (Зловоние, i, j + 1) находится (Зловоние, i-1, j)

находится (Зловоние, i+1, j); (4.17)*

находится (Зловоние, i, j) находится (Чудовище, i, j)

находится (Чудовище, i, j -1) находится (Чудовище, i, j +1)

находится (Чудовище, i-1, j) находится (Чудовище, i + 1, j); (4.18)*

находится (Сквозняк, i, j) находится (Яма, i, j-1)

находится (Яма, i, j + 1) находится (Яма, i-1, j)

находится (Яма, i+1, j), (4.19)*

С помощью преобразования

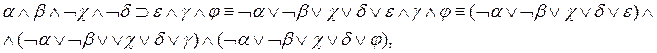удаления квантора существования и правила исключения конъюнкта получаем следующие формулы:

находится (Агент, i, j) ориентация (i, j-1)

находится (Чудовище, i, j-1) находится (Яма, i, j-1)

перейти (i, j-1);

находится (Агент, i, j) ориентация (i, j-1)

находится (Чудовище, i, j-1) находится (Яма, i, j-1)

находится (Агент, i, j-1);

находится (Агент, i, j) ориентация (i, j-1)

находится (Чудовище, i, j-1) находится (Яма, i, j-1)

ориентация (i, j-2). (4.20)*

Число подформул в системе формул (4.20)* совпадает с числом литералов вследствие импликативной формулы (4.20) и различаются они только последним литералом. Поэтому для остальных формул (4.21)* - (4.23)* выпишем только первую подформулу:

находится (Агент, i, j) ориентация (i, j + 1)

находится (Чудовище, i, j + 1) находится (Яма, i, j +1)

перейти (i, j + 1); (4.21)*

находится (Агент, i, j) ориентация (i-1, j)

находится (Чудовище, i-1, j) находится (Яма, i-1, j)

перейти (i-1, j); (4.22)*

находится (Агент, i, j) ориентация (i + 1, j)

находится (Чудовище, i + 1, j) находится (Яма, i + 1, j)

перейти (i+1, j); (4.23)*

находится (Агент, i, j) находится (Блеск, i, j) взять (i, j). (4.24)*

Подформулы системы формул (4.25)* — (4.32)* получаются аналогично, но их еще больше. Выпишем, как и в предыдущем случае, только по одной (первой) подформуле:

находится (Агент, i, j) ориентация (i, j-1)

находится (Чудовище, i, j-1) v повернуться_направо (i, j); (4.25)*

находится (Агент, i, j) ориентация (i-1,j)

находится (Чудовище, i-1, j) повернуться_направо (i, j); (4.26)*

находится (Агент, i, j) ориентация (i, j + 1)

находится (Чудовище, i, j + 1) повернуться_направо (i, j); (4.27)*

находится (Агент, i, j) ориентация (i+1, j)

находится (Чудовище, i+1,j) повернуться_направо (i, j + 1); (4.28)*

находится (Агент, i, j) ориентация (i, j-1)

находится (Чудовище, i, j-1) повернуться_налево (i, j); (4.29)*

находится (Агент, i, j) ориентация (i-1, j)

находится (Чудовище, i-1, j) повернуться_налево (i,j); (4.30)*

находится (Агент, i, j) ориентация (i, j + 1)

находится (Чудовище, i, j + 1) повернуться_налево (i, j); (4.31)*

находится (Агент, i, j) ориентация (i+1, j)

находится (Чудовище, i+1,j) повернуться_ налево (i, j). (4.32)*

Применение обобщенного правила модус поненс вследствие того, что в нем используются не отдельные атомы, а их конъюнкции, делает вывод более эффективным. Это объясняется тем, что подстановка одних и тех же констант осуществляется сразу для совокупности атомов, входящих в конъюнкцию левой части импликации и, если необходимо, то правой.